题目内容
（2003•无锡）已知：如图，△ABC中，AB=AC，AD⊥BC于点D，E是AD延长线上一点，连BE、CE．求证：BE=CE．
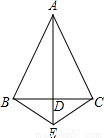
【答案】分析：由AB=AC，AD⊥BC得到AD是BC的中垂线，由中垂线的性质：中垂线上的点到线段的两个端点的距离相等知，BE=CE．
解答：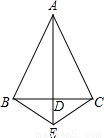
证明：证法1：
∵AB=AC，AD⊥BC，
∴BD=DC．（2分）
∴AD为BC的中垂线．（4分）
∴BE=EC．（6分）
证法2：
∵AB=AC，AD⊥BC，
∴∠BAE=∠CAE．（2分）
在△ABE与△ACE中，
，
∴△ABE≌△ACE（SAS）．（4分）
∴BE=CE．（6分）
点评：本题利用了中垂线的判定和性质证明；也可利用三角形全等的判定证明．
解答：
证明：证法1：∵AB=AC，AD⊥BC，
∴BD=DC．（2分）
∴AD为BC的中垂线．（4分）
∴BE=EC．（6分）
证法2：
∵AB=AC，AD⊥BC，
∴∠BAE=∠CAE．（2分）
在△ABE与△ACE中，
，∴△ABE≌△ACE（SAS）．（4分）
∴BE=CE．（6分）
点评：本题利用了中垂线的判定和性质证明；也可利用三角形全等的判定证明．
练习册系列答案
相关题目
，抛物线的顶点为点P，是否存在这样的抛物线，使得△PAB的外接圆半径为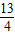
？若存在，求出这样的抛物线的解析式；若不存在，请说明理由．
，抛物线的顶点为点P，是否存在这样的抛物线，使得△PAB的外接圆半径为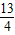
？若存在，求出这样的抛物线的解析式；若不存在，请说明理由．
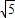，tanB=
．
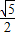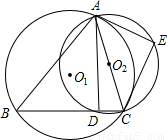
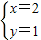是关于x、y的方程2x-y+3k=0的解，则k= ．