题目内容
(2003•黄石)先阅读下面一段材料,再完成后面的问题:材料:过抛物线y=ax2(a>0)的对称轴上一点(0,-
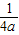 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0, )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
).问题:若直线y=kx+b交抛物线y=
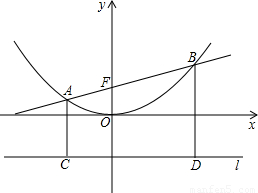
 x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).①求抛物线y=
 x2的焦点F的坐标;
x2的焦点F的坐标;②求证:直线AB过焦点时,CF⊥DF;
③当直线AB过点(-1,0),且以线段AB为直径的圆与准线l相切时,求这条直线对应的函数解析式.
【答案】分析:①将a= 代入题中给出的焦点坐标公式中即可.
代入题中给出的焦点坐标公式中即可.
②根据焦点的概念可知:AC=AF,BF=BD,如果连接CF、DF,那么CF必平分角AFO(可用三角形全等证出).同理可求得DF平分∠BFO,由此可得证.
③可连接圆心与切点,设圆心为M,切点为N,那么MN就是梯形ACDB的中位线,因此MN= (AC+BD)=
(AC+BD)= AB,根据焦点的定义知:AF=AC,BF=BD,因此AF+BF=AB,也就是说直线AB恰好过焦点F,那么可根据F的坐标(①已求得)和已知的点(-1,0)的坐标用待定系数法求出抛物线的解析式.
AB,根据焦点的定义知:AF=AC,BF=BD,因此AF+BF=AB,也就是说直线AB恰好过焦点F,那么可根据F的坐标(①已求得)和已知的点(-1,0)的坐标用待定系数法求出抛物线的解析式.
解答:①解:F(0,1)
②证明:∵AC=AF,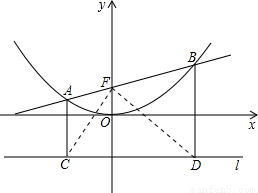
∴∠ACF=∠AFC
又∵AC∥OF,
∴∠ACF=∠CFO,
∴CF平分∠AFO,同理DF平分∠BFO;
而∠AFO+∠BFO=180°
∴∠CFO+∠DFO= (∠AFO+∠BFO)=90°;
(∠AFO+∠BFO)=90°;
∴CF⊥DF.
③解:设圆心为M,且与l的切点为N,连接MN;
∴MN= AB
AB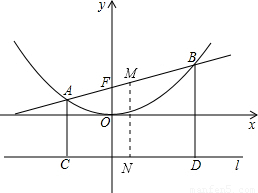
在直角梯形ACDB中,M是AB的中点.
∴MN= (AC+BD),而AC=AF,BD=BF.
(AC+BD),而AC=AF,BD=BF.
∴MN= (AF+BF)
(AF+BF)
∴AF+BF=AB
∴AB过焦点F(0,1).
又AB过点(-1,0)
∴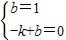
解得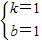
∴AB对应的函数解析式为y=x+1.
点评:本题为阅读类题,解题的关键是弄清材料中各定义的含义,然后结合自己掌握的知识进行求解.
 代入题中给出的焦点坐标公式中即可.
代入题中给出的焦点坐标公式中即可.②根据焦点的概念可知:AC=AF,BF=BD,如果连接CF、DF,那么CF必平分角AFO(可用三角形全等证出).同理可求得DF平分∠BFO,由此可得证.
③可连接圆心与切点,设圆心为M,切点为N,那么MN就是梯形ACDB的中位线,因此MN=
 (AC+BD)=
(AC+BD)= AB,根据焦点的定义知:AF=AC,BF=BD,因此AF+BF=AB,也就是说直线AB恰好过焦点F,那么可根据F的坐标(①已求得)和已知的点(-1,0)的坐标用待定系数法求出抛物线的解析式.
AB,根据焦点的定义知:AF=AC,BF=BD,因此AF+BF=AB,也就是说直线AB恰好过焦点F,那么可根据F的坐标(①已求得)和已知的点(-1,0)的坐标用待定系数法求出抛物线的解析式.解答:①解:F(0,1)
②证明:∵AC=AF,

∴∠ACF=∠AFC
又∵AC∥OF,
∴∠ACF=∠CFO,
∴CF平分∠AFO,同理DF平分∠BFO;
而∠AFO+∠BFO=180°
∴∠CFO+∠DFO=
 (∠AFO+∠BFO)=90°;
(∠AFO+∠BFO)=90°;∴CF⊥DF.
③解:设圆心为M,且与l的切点为N,连接MN;
∴MN=
 AB
AB
在直角梯形ACDB中,M是AB的中点.
∴MN=
 (AC+BD),而AC=AF,BD=BF.
(AC+BD),而AC=AF,BD=BF.∴MN=
 (AF+BF)
(AF+BF)∴AF+BF=AB
∴AB过焦点F(0,1).
又AB过点(-1,0)
∴
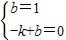
解得
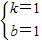
∴AB对应的函数解析式为y=x+1.
点评:本题为阅读类题,解题的关键是弄清材料中各定义的含义,然后结合自己掌握的知识进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )作对称轴的垂线l,则抛物线上任意一点P到点F(0,
)作对称轴的垂线l,则抛物线上任意一点P到点F(0,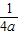 )的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0,
)的距离与P到l的距离一定相等,我们将点F与直线l分别称作这抛物线的焦点和准线,如y=x2的焦点为(0, ).
). x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图).
x2于A、B、AC、BD垂直于抛物线的准线l,垂直足分别为C、D(如图). x2的焦点F的坐标;
x2的焦点F的坐标;