题目内容
已知:如图,DG⊥BC AC⊥BC,EF⊥AB,∠1=∠2.求证:EF∥CD
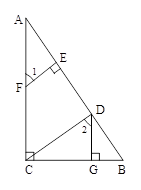
证明:∵ DG⊥BC,AC⊥BC( )
∴ ∠DGB=∠ACB=90º(垂直的定义)
∴ DG∥AC ( )
∴ ∠2 = ( )
∵ ∠1=∠2 ( )
∴ ∠1=∠DCA(等量代换)
∴ EF∥CD ( )

证明:∵ DG⊥BC,AC⊥BC( )
∴ ∠DGB=∠ACB=90º(垂直的定义)
∴ DG∥AC ( )
∴ ∠2 = ( )
∵ ∠1=∠2 ( )
∴ ∠1=∠DCA(等量代换)
∴ EF∥CD ( )
已知 , 同位角相等,两直线平行,∠DCA,两直线平行,内错角相等,已知,同位角相等,两直线平行,
专题:推理填空题。
分析:灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质证明即可。
解答:
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC(同位角相等,两直线平行)
∴∠2=∠ACD(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠1=∠ACD(等量代换)
∴EF∥CD(同位角相等,两直线平行)
点评:利用垂直的定义除了由垂直得直角外,还能由直角判定垂直,判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法。

练习册系列答案
相关题目

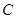 是线段
是线段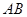 的黄金分割点
的黄金分割点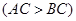 ,下列结论错误的是( )
,下列结论错误的是( )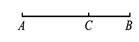
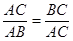
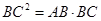



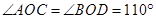 ,
,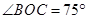
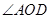 的度数
的度数