题目内容
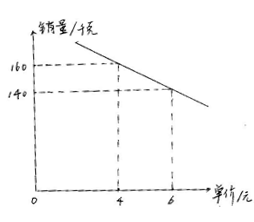
(本题满分10分)某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件
(1)假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x间的函数关系式,并注明x的取值范围.
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
(1)y=100(-x2+6x+55)(0<x≤1)
(2)销售单价为10.5元时利润最大,最大利润为6400元
解析(1)解:设降价x元时利润最大.依题意:y=(13.5-x-2.5)(500+100x)…2分
整理得:y=100(-x2+6x+55)(0<x≤1)………5分
(2)由(1)可知,当x=3时y取最大值,最大值是6400………7分
即降价3元时利润最大,∴销售单价为10.5元时,最大利润6400元.…………9分
答:销售单价为10.5元时利润最大,最大利润为6400元…………10分

练习册系列答案
相关题目
(本题满分10分)某商店代销一批季节性服装,每套代销成本40元,第一个月每套销售定价为52元时,可售出180套;应市场变化调整第一个月的销售价,预计销售定价每增加1元,销售量将减少10套。
(1)若设第二个月的销售定价每套增加x元,填写下表。
| 时间 | 第一个月 | 第二个月 |
| 每套销售定价(元) |
|
|
| 销售量(套) |
|
|
(2)若商店预计要在这两个月的代销中获利4160元,则第二个月销售定价每套多少元?