题目内容
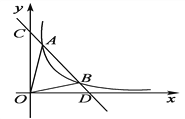
【题目】如图,在平面直角坐标系中,![]() 两点分别是
两点分别是![]() 轴和
轴和![]() 轴正半轴上两个动点,以三点
轴正半轴上两个动点,以三点![]() 为顶点的矩形
为顶点的矩形![]() 的面积为24,反比例函数
的面积为24,反比例函数![]() (
(![]() 为常数且
为常数且![]() )的图象与矩形
)的图象与矩形![]() 的两边
的两边![]() 分别交于点
分别交于点![]() .
.
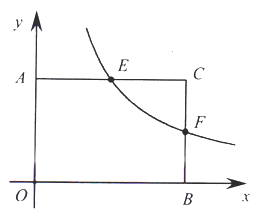
(1)若![]() 且点
且点![]() 的横坐标为3.
的横坐标为3.
①点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 (不需写过程,直接写出结果);
的坐标为 (不需写过程,直接写出结果);
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的周长最小?若存在,请求出
的周长最小?若存在,请求出![]() 的周长最小值;若不存在,请说明理由.
的周长最小值;若不存在,请说明理由.
(2)连接![]() ,在点
,在点![]() 的运动过程中,
的运动过程中,![]() 的面积会发生变化吗?若变化,请说明理由,若不变,请用含
的面积会发生变化吗?若变化,请说明理由,若不变,请用含![]() 的代数式表示出
的代数式表示出![]() 的面积.
的面积.
【答案】(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;②存在,周长
;②存在,周长![]() ;
;
(2)不变,![]() 的面积为
的面积为![]()
【解析】
(1)①求出点E的坐标,得出C点的纵坐标,根据面积为24即可求出C的坐标,得出F点横坐标即可求解;
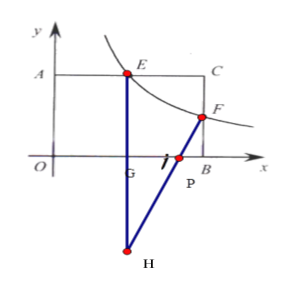
②作点E关于x轴的对称点G,连接GF,与x轴的交点为p,此时![]() 的周长最小
的周长最小
(2)先算出三角形![]() 与三角形
与三角形![]() 的面积,再求出三角形
的面积,再求出三角形![]() 的面积即可.
的面积即可.
(1)①点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ;
;
②作点E关于x轴的对称点G,连接GF,求与x轴的交点为p,此时![]() 的周长最小
的周长最小
由①得EF=![]()
由对称可得EP=PH,
由 H(3,-4) F(6,2)可得HF=3![]()
△PEF=EP+PF+EF=FH+EF=![]()
(2)不变,求出三角形![]() 与三角形
与三角形![]() 的面积为
的面积为![]()
求出三角形![]() 的面积为
的面积为![]()
求出三角形![]() 的面积为
的面积为![]()
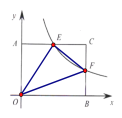
设E位(a, ![]() ),则S△AEO=
),则S△AEO=![]() ,同理可得S△AFB=
,同理可得S△AFB=![]() ,
,
∵矩形![]() 的面积为24
的面积为24
F(![]() ,
,![]() ),C(
),C(![]() ,
,![]() )
)
S△CEF=![]()
![]()
S![]() =24-
=24-![]() -k=
-k=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.