题目内容
(2012•静海县二模)已知二次函数y1=ax2+bx+c(a≠0)的图象经过三点(1,0),(-3,0),(0,-
).
(Ⅰ)求二次函数的解析式;
(Ⅱ)若(Ⅰ)中的二次函数,当x取a,b(a≠b)时函数值相等,求x取a+b时的函数值;
(Ⅲ)若反比例函数y2=
(k>0,x>0)的图象与(Ⅰ)中的二次函数的图象在第一象限内的交点为A,点A的横坐标为x0满足2<x0<3,试求实数k的取值范围.
| 3 |
| 2 |
(Ⅰ)求二次函数的解析式;
(Ⅱ)若(Ⅰ)中的二次函数,当x取a,b(a≠b)时函数值相等,求x取a+b时的函数值;
(Ⅲ)若反比例函数y2=
| k |
| x |
分析:(Ⅰ)直接利用待定系数法求函数的解析式即可.
(Ⅱ)首先将x=a、b代入抛物线的解析式中,联立所得的两个方程即可求出a+b的值;再将x=a+b代入(Ⅰ)的抛物线解析式中即可求出此时的函数值.
(Ⅲ)首先大致画出y1、y2的函数图象,大致判断出2<x0<3中,两函数的增减性;然后根据x0=2或3时,两函数值的大小关系列出不等式组,由此求得k的取值范围.
(Ⅱ)首先将x=a、b代入抛物线的解析式中,联立所得的两个方程即可求出a+b的值;再将x=a+b代入(Ⅰ)的抛物线解析式中即可求出此时的函数值.
(Ⅲ)首先大致画出y1、y2的函数图象,大致判断出2<x0<3中,两函数的增减性;然后根据x0=2或3时,两函数值的大小关系列出不等式组,由此求得k的取值范围.
解答:解:(Ⅰ)设抛物线解析式为y=a(x-1)(x+3)
将(0,-
)代入,解得a=
.
∴抛物线解析式为y=
x2+x-
.
(Ⅱ)当x=a时,y1=
a2+a-
,当x=b时,y1=
b2+b-
,
∴
a2+a-
=
b2+b-
,
∴a2-b2+2(a-b)=0,即(a-b)(a+b+2)=0,
∵a≠b,∴a+b=-2.
∴y1=
(a+b)2+(a+b)-
=
(-2)2-2-
=-
即x取a+b时的函数值为-
.
(Ⅲ)当2<x<3时,函数y1=
x2+x-
,y1随着x增大而增大,对y2=
(k>0),y2随着X的增大而减小.
∵A(x0,y0)为二次函数图象与反比例函数图象的交点,
∴当x0=2时,由反比例函数图象在二次函数上方得y2>y1,
即
>
×22+2-
,解得k>5.
当x0=3时,二次函数数图象在反比例上方得y1>y2,
即
×32+3-
>
,解得k<18.
所以k的取值范围为5<k<18.
将(0,-
| 3 |
| 2 |
| 1 |
| 2 |
∴抛物线解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅱ)当x=a时,y1=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴a2-b2+2(a-b)=0,即(a-b)(a+b+2)=0,
∵a≠b,∴a+b=-2.
∴y1=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
即x取a+b时的函数值为-
| 3 |
| 2 |
(Ⅲ)当2<x<3时,函数y1=
| 1 |
| 2 |
| 3 |
| 2 |
| k |
| x |
∵A(x0,y0)为二次函数图象与反比例函数图象的交点,
∴当x0=2时,由反比例函数图象在二次函数上方得y2>y1,
即
| k |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当x0=3时,二次函数数图象在反比例上方得y1>y2,
即
| 1 |
| 2 |
| 3 |
| 2 |
| k |
| 3 |
所以k的取值范围为5<k<18.
点评:该题主要考查的是函数解析式的确定以及不等式的应用.最后一题中,通过图示找出与题相关的不等式是突破题目的关键,因此在平常的解题过程中,要注意数形结合思想的合理运用.

练习册系列答案
相关题目
 (2012•静海县二模)如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )
(2012•静海县二模)如图,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1,与x轴的另一个交点为A1.若四边形AC1A1C为矩形,则a,b应满足的关系式为( )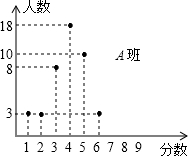 (2012•静海县二模)现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0、1、2、3、4、5、6、7、8、9分这几种不同分值中的一种.测试结果A班的成绩如下图所示,B班的成绩如表所示.
(2012•静海县二模)现有A、B两个班级,每个班级各有45名学生参加一次测验,每名参加者可获得0、1、2、3、4、5、6、7、8、9分这几种不同分值中的一种.测试结果A班的成绩如下图所示,B班的成绩如表所示.