题目内容
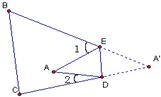
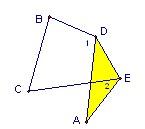8、如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外部时，则∠A与∠1和∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）分析：此题求的是∠A、∠1、∠2之间的数量关系，首先画出折叠前的三角形，设为△BCF，可根据三角形的外角性质，首先表示出∠DEF的度数，进而根据三角形内角和定理，得到所求的结论．
解答：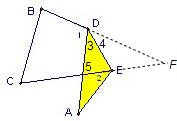
解：如右图，设翻折前A点的对应点为F；
根据折叠的性质知：∠3=∠4，∠F=∠A；
由三角形的外角性质知：∠DEF=∠5+∠3=∠A+∠2+∠3；
△DEF中，∠DEF=180°-∠4-∠F；
故180°-∠4-∠F=∠A+∠2+∠3，即：
180°-∠4-∠A=∠A+∠2+∠3，
180°-∠4-∠3=2∠A+∠2，即∠1=2∠A+∠2，2∠A=∠1-∠2，
故选B．
解：如右图，设翻折前A点的对应点为F；根据折叠的性质知：∠3=∠4，∠F=∠A；
由三角形的外角性质知：∠DEF=∠5+∠3=∠A+∠2+∠3；
△DEF中，∠DEF=180°-∠4-∠F；
故180°-∠4-∠F=∠A+∠2+∠3，即：
180°-∠4-∠A=∠A+∠2+∠3，
180°-∠4-∠3=2∠A+∠2，即∠1=2∠A+∠2，2∠A=∠1-∠2，
故选B．
点评：此题主要考查了图形的翻折变换、三角形内角和定理以及三角形的外角性质，正确作出辅助线是解答此题的关键．
练习册系列答案
相关题目
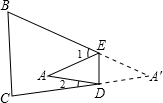如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，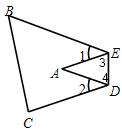
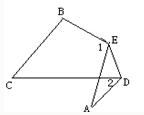20、如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外部时，∠A与∠1、∠2之间存在一种始终保持不变的数量关系，这个数量关系是
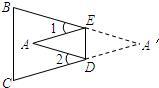如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，