题目内容
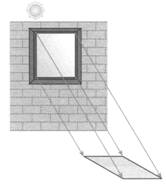
 阳光透过长方形玻璃窗投射到地面上,地面上会出现一个明亮的四边形,用量角器量出这个四边形的一个锐角恰好是30°,又用直尺量出一组邻边的长分别是40cm和55cm,那么地面上的四边形面积和周长分别为
阳光透过长方形玻璃窗投射到地面上,地面上会出现一个明亮的四边形,用量角器量出这个四边形的一个锐角恰好是30°,又用直尺量出一组邻边的长分别是40cm和55cm,那么地面上的四边形面积和周长分别为
- A.1512.5 cm2;95 cm
- B.550 cm2;190 cm
- C.1100 cm2;190 cm
- D.800 cm2;190 cm
C
分析:根据平行四边形的性质对边相等可以求出四边形的周长,再利用锐角三角函数关系求出平行四边形的高,即可得出平行四边形的面积.
解答: 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,
由题意得出;四边形的周长为:2(AD+AB)=2×(40+55)=190(cm),
∵∠A=30°,
∴sin30°= =
= ,
,
解得:DE=20,
故四边形面积为:55×20=1100(cm 2),
故选:C.
点评:此题主要考查了平行四边形的性质,根据已知得出平行四边形的高是解题关键.
分析:根据平行四边形的性质对边相等可以求出四边形的周长,再利用锐角三角函数关系求出平行四边形的高,即可得出平行四边形的面积.
解答:
 解:过点D作DE⊥AB于点E,
解:过点D作DE⊥AB于点E,由题意得出;四边形的周长为:2(AD+AB)=2×(40+55)=190(cm),
∵∠A=30°,
∴sin30°=
 =
= ,
,解得:DE=20,
故四边形面积为:55×20=1100(cm 2),
故选:C.
点评:此题主要考查了平行四边形的性质,根据已知得出平行四边形的高是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 阳光透过长方形玻璃窗投射到地面上,地面上会出现一个明亮的四边形,用量角器量出这个四边形的一个锐角恰好是30°,又用直尺量出一组邻边的长分别是40cm和55cm,那么地面上的四边形面积和周长分别为( )
阳光透过长方形玻璃窗投射到地面上,地面上会出现一个明亮的四边形,用量角器量出这个四边形的一个锐角恰好是30°,又用直尺量出一组邻边的长分别是40cm和55cm,那么地面上的四边形面积和周长分别为( )