题目内容
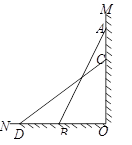
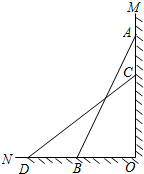 如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4m吗?为什么?
分析:(1)在Rt△AOB中利用勾股定理求得AO的长即可;
(2)在梯子长度不变的情况下,求出DO的长后减去BO的长求得BD即可作出判断.
(2)在梯子长度不变的情况下,求出DO的长后减去BO的长求得BD即可作出判断.
解答:解:(1)∵AO⊥DO,
∴AO=
,
=
,
=12m,
∴梯子顶端距地面12m高;
(2)滑动不等于4m,
∵AC=4m,
∴OC=AO-AC=8m,
∴OD=
,
=
=
m,
∴BD=OD-OB=
-5>4,
∴滑动不等于4m.
∴AO=
| AB2-BO2 |
=
| 132-52 |
=12m,
∴梯子顶端距地面12m高;
(2)滑动不等于4m,
∵AC=4m,
∴OC=AO-AC=8m,
∴OD=
| CD2-OC2 |
=
| 132-82 |
| 105 |
∴BD=OD-OB=
| 105 |
∴滑动不等于4m.
点评:本题考查了勾股定理的应用,解题的关键是在直角三角形中弄清直角边和斜边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目