题目内容
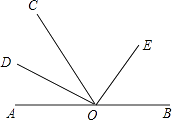
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 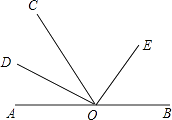
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
【答案】
(1)∠BOE、∠COE
(2)解:∵OD、OE分别平分∠AOC、∠BOC,∠AOC=72°,
∴∠COD=∠AOD=36°,∠COE=∠BOE= ![]() ∠BOC,
∠BOC,
∴∠BOC=180°﹣72°=108°,
∴∠COE= ![]() ∠BOC=54°,
∠BOC=54°,
∴∠DOE=∠COD+∠COE=90°
(3)解:当∠AOD=x°时,∠DOE=90°
【解析】解:(1)∵OE平分∠BOC,
∴∠BOE=∠COE;
∵∠AOE+∠BOE=180°,
∴∠AOE+∠COE=180°,
∴与∠AOE互补的角是∠BOE、∠COE;
所以答案是∠BOE、∠COE;
【考点精析】本题主要考查了余角和补角的特征的相关知识点,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关才能正确解答此题.

练习册系列答案
相关题目