题目内容
(2006•太原)某地计划开凿一条单向行驶(从正中通过)的隧道,其截面是抛物线拱形ACB,而且能通过最宽3米,最高3.5米的厢式货车.按规定,机动车通过隧道时车身距隧道壁的水平距离和铅直距离最小都是0.5米.为设计这条能使上述厢式货车恰好安全通过的隧道,在图纸上以直线AB为x轴,线段AB的垂直平分线为y轴,建立如图所示的直角坐标系,求抛物线拱形的表达式、隧道的跨度AB和拱高OC.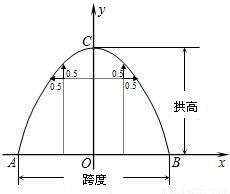
【答案】分析:根据建立的坐标系可设表达式为y=ax2+h,因为图象过(1.5,4)和(2,3.5),所以可求解析式,再根据解析式求解.
解答:解:设抛物线的表达式为y=ax2+h,
∵图象经过点(1.5,4)和(2,3.5),
∴ ,
,
解之得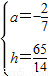 .
.
故抛物线的表达式为y=- x2+
x2+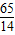 ,
,
拱高OC即是当x=0时y的值为 米.
米.
当y=0时有- x2+
x2+ =0
=0
解之得x1= ,x2=-
,x2=- .
.
即是A、B两点的横坐标,
故可得跨度AB= 米.
米.
点评:通过建模把实际问题转化为数学问题是运用数学知识解决实际问题的常用手段,重在根据题意建立适当的数学模型.
解答:解:设抛物线的表达式为y=ax2+h,
∵图象经过点(1.5,4)和(2,3.5),
∴
 ,
,解之得
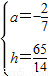 .
.故抛物线的表达式为y=-
 x2+
x2+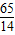 ,
,拱高OC即是当x=0时y的值为
 米.
米.当y=0时有-
 x2+
x2+ =0
=0解之得x1=
 ,x2=-
,x2=- .
.即是A、B两点的横坐标,
故可得跨度AB=
 米.
米.点评:通过建模把实际问题转化为数学问题是运用数学知识解决实际问题的常用手段,重在根据题意建立适当的数学模型.

练习册系列答案
相关题目
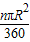 ,并通过比较扇形面积公式与弧长公式l=
,并通过比较扇形面积公式与弧长公式l= ,得出扇形面积的另一种计算方法S扇形=
,得出扇形面积的另一种计算方法S扇形= lR.接着老师让同学们解决两个问题:
lR.接着老师让同学们解决两个问题: lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S=
lR类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S= (l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
(l1+l2)d.他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.
