ЬтФПФкШн
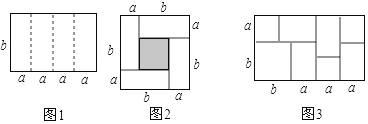
ЁОЬтФПЁПШчЭМ1ЪЧвЛИіГЄЮЊ4aЁЂПэЮЊbЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖЦНОљЗжГЩЫФПщаЁГЄЗНаЮЃЌШЛКѓгУЫФПщаЁГЄЗНаЮЦДГЩвЛИіЁАЛиаЮЁБе§ЗНаЮЃЈШчЭМ2ЃЉ
ЃЈ1ЃЉЙлВьЭМ2ЧыФуаДГіЃЈa+bЃЉ2ЁЂЃЈaЉbЃЉ2ЁЂabжЎМфЕФЕШСПЙиЯЕЪЧ_____ЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉжаЕФНсТлЃЌШєx+y=5ЃЌxy=![]() ЃЌдђxЉy=______ЃЛ
ЃЌдђxЉy=______ЃЛ
ЃЈ3ЃЉШєЃЈ3xЉ2yЃЉ2=5ЃЌЃЈ3x+2yЃЉ2=9ЃЌЧѓxyЕФжЕЃЎ
ЃЈ4ЃЉЪЕМЪЩЯЭЈЙ§МЦЫуЭМаЮЕФУцЛ§ПЩвдЬНЧѓЯргІЕФЕШЪНЃЎШчЭМ3ЃЌФугаЪВУДЗЂЯжЃП_____ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈa+bЃЉ2-ЃЈaЉbЃЉ2=4abЃЛЃЈ2ЃЉЁР4ЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2.
ЃЛЃЈ4ЃЉЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2.
ЁОНтЮіЁП
ЃЈ1ЃЉдкЭМ2жаЃЌДѓе§ЗНаЮгЩаЁе§ЗНаЮКЭ4ИіОиаЮзщГЩЃЌдђЃЈa+bЃЉ2-ЃЈa-bЃЉ2=4abЃЛЃЈ2ЃЉгЩЃЈ1ЃЉЕФНсТлЕУЕНЃЈx+yЃЉ2-ЃЈx-yЃЉ2=4xyЃЌдйАбx+y=5ЃЌxy=![]() ДњШыЃЌШЛКѓРћгУЦНЗНИљЕФЖЈвхЧѓНтМДПЩЃЛЃЈ3ЃЉАбЃЈ3x+2yЃЉ2БфаЮЮЊЃЈ3xЉ2yЃЉ2+4ЁС3x
ДњШыЃЌШЛКѓРћгУЦНЗНИљЕФЖЈвхЧѓНтМДПЩЃЛЃЈ3ЃЉАбЃЈ3x+2yЃЉ2БфаЮЮЊЃЈ3xЉ2yЃЉ2+4ЁС3x![]() 2yЕФаЮЪНЃЌдйДњШыЃЈ3x+2yЃЉ2гыЃЈ3xЉ2yЃЉ2ЕФжЕЃЌМДПЩЧѓГіxyЕФжЕЃЛЃЈ4ЃЉЙлВьЭМаЮЕУЕНБпГЄЮЊЃЈa+bЃЉгыЃЈ3a+bЃЉЕФОиаЮгЩ3ИіБпГЄЮЊaЕФе§ЗНаЮЁЂ4ИіБпГЄЮЊaЁЂbЕФОиаЮКЭвЛИіБпГЄЮЊbЕФе§ЗНаЮзщГЩЃЌдђгаЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2ЃЎ
2yЕФаЮЪНЃЌдйДњШыЃЈ3x+2yЃЉ2гыЃЈ3xЉ2yЃЉ2ЕФжЕЃЌМДПЩЧѓГіxyЕФжЕЃЛЃЈ4ЃЉЙлВьЭМаЮЕУЕНБпГЄЮЊЃЈa+bЃЉгыЃЈ3a+bЃЉЕФОиаЮгЩ3ИіБпГЄЮЊaЕФе§ЗНаЮЁЂ4ИіБпГЄЮЊaЁЂbЕФОиаЮКЭвЛИіБпГЄЮЊbЕФе§ЗНаЮзщГЩЃЌдђгаЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2ЃЎ
ЃЈ1ЃЉЁпЭМ2жавѕгАВПЗжЮЊБпГЄЮЊЃЈb-aЃЉЕФе§ЗНаЮЃЌ
ЁрвѕгАВПЗжЕФУцЛ§ЃЈb-aЃЉ2ЃЌ
ЁпБпГЄЮЊa+bЕФе§ЗНаЮЕФУцЛ§МѕШЅБпГЄЮЊb-aЕФе§ЗНаЮЕШгк4ИіГЄПэЗжБ№aЁЂbЕФОиаЮУцЛ§ЃЌ
ЁрЃЈa+bЃЉ2-ЃЈaЉbЃЉ2=4abЃЌ
ЙЪД№АИЮЊЃКЃЈa+bЃЉ2-ЃЈaЉbЃЉ2=4ab
ЃЈ2ЃЉгЩЃЈ1ЃЉЕУЃЈx+yЃЉ2-ЃЈx-yЃЉ2=4xyЃЌ
Ёпx+y=5ЃЌxy=![]() ЃЌ
ЃЌ
Ёр25-ЃЈx-yЃЉ2=9ЃЌ
ЁрЃЈx-yЃЉ2=16ЃЌ
Ёрx-y=ЁР4ЃЌ
ЙЪД№АИЮЊЃКЁР4
ЃЈ3ЃЉгЩЃЈ1ЃЉЕУЃЈ3x+2yЃЉ2=ЃЈ3xЉ2yЃЉ2+4ЁС3x![]() 2y
2y
ЁпЃЈ3xЉ2yЃЉ2=5ЃЌЃЈ3x+2yЃЉ2=9ЃЌ
Ёр9=5+24xyЃЌ
Ёрxy=![]() .
.
ЃЈ4ЃЉБпГЄЮЊЃЈa+bЃЉгыЃЈ3a+bЃЉЕФОиаЮУцЛ§ЮЊЃЈa+bЃЉЃЈ3a+bЃЉЃЌЫќгЩ3ИіБпГЄЮЊaЕФе§ЗНаЮЁЂ4ИіБпГЄЮЊaЁЂbЕФОиаЮКЭвЛИіБпГЄЮЊbЕФе§ЗНаЮзщГЩЃЌ
ЁрЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2ЃЎ
ЙЪД№АИЮЊЃКЃЈa+bЃЉЃЈ3a+bЃЉ=3a2+4ab+b2










