题目内容
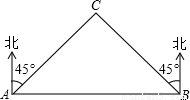
 如图,已知在东西走向的海岸线上有相距8n mile的两座灯塔A和B,有一只船在灯塔A的北偏东45°方向,而同时在灯塔B的北偏西45°方向的C点以每小时20n mile的速度向东航行,那么该船再航行____min,离灯塔B最近.
如图,已知在东西走向的海岸线上有相距8n mile的两座灯塔A和B,有一只船在灯塔A的北偏东45°方向,而同时在灯塔B的北偏西45°方向的C点以每小时20n mile的速度向东航行,那么该船再航行____min,离灯塔B最近.
- A.4
- B.6
- C.12
- D.13
C
分析:CD⊥AB于D点,CE垂直于B点的正北方向,则点E为离灯塔B最近点,根据方向角易得∠CAB=90°-45°=45°,∠CBA=90°-45°=45°,则△ACB为等腰直角三角形,根据其性质得到
BD= AB=
AB= ×8=4,再证四边形BECD为矩形,则CE=DB=4,然后根据速度公式得到从C点到E点所用的时间=
×8=4,再证四边形BECD为矩形,则CE=DB=4,然后根据速度公式得到从C点到E点所用的时间=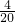 ×60=12(分).
×60=12(分).
解答:如图,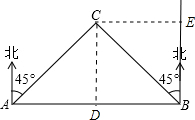 CD⊥AB于D点,CE垂直于B点的正北方向,即点E为离灯塔B最近点,
CD⊥AB于D点,CE垂直于B点的正北方向,即点E为离灯塔B最近点,
∵C点在点A的北偏东45°方向,点B的北偏西45°方向,
∴∠CAB=90°-45°=45°,∠CBA=90°-45°=45°,
∴∠ACB=180°-45°-45°=90°,
∴△ACB为等腰直角三角形,
∵CD⊥AB,
∴BD= AB=
AB= ×8=4,
×8=4,
∵∠CDB=∠DBE=∠BEC=90°,
∴四边形BECD为矩形,
∴CE=DB=4,
∴从C点到E点所用的时间=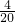 ×60=12(分).
×60=12(分).
故选C.
点评:本题考查了等腰直角三角形的性质:等腰直角三角形的两底角都为45°,斜边上的高平分斜边,并且等于斜边的一半.也考查了方向角.
分析:CD⊥AB于D点,CE垂直于B点的正北方向,则点E为离灯塔B最近点,根据方向角易得∠CAB=90°-45°=45°,∠CBA=90°-45°=45°,则△ACB为等腰直角三角形,根据其性质得到
BD=
 AB=
AB= ×8=4,再证四边形BECD为矩形,则CE=DB=4,然后根据速度公式得到从C点到E点所用的时间=
×8=4,再证四边形BECD为矩形,则CE=DB=4,然后根据速度公式得到从C点到E点所用的时间=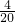 ×60=12(分).
×60=12(分).解答:如图,
 CD⊥AB于D点,CE垂直于B点的正北方向,即点E为离灯塔B最近点,
CD⊥AB于D点,CE垂直于B点的正北方向,即点E为离灯塔B最近点,∵C点在点A的北偏东45°方向,点B的北偏西45°方向,
∴∠CAB=90°-45°=45°,∠CBA=90°-45°=45°,
∴∠ACB=180°-45°-45°=90°,
∴△ACB为等腰直角三角形,
∵CD⊥AB,
∴BD=
 AB=
AB= ×8=4,
×8=4,∵∠CDB=∠DBE=∠BEC=90°,
∴四边形BECD为矩形,
∴CE=DB=4,
∴从C点到E点所用的时间=
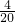 ×60=12(分).
×60=12(分).故选C.
点评:本题考查了等腰直角三角形的性质:等腰直角三角形的两底角都为45°,斜边上的高平分斜边,并且等于斜边的一半.也考查了方向角.

练习册系列答案
相关题目
 如图,已知在东西走向的海岸线上有相距8n mile的两座灯塔A和B,有一只船在灯塔A的北偏东45°方向,而同时在灯塔B的北偏西45°方向的C点以每小时20n mile的速度向东航行,那么该船再航行( )min,离灯塔B最近.
如图,已知在东西走向的海岸线上有相距8n mile的两座灯塔A和B,有一只船在灯塔A的北偏东45°方向,而同时在灯塔B的北偏西45°方向的C点以每小时20n mile的速度向东航行,那么该船再航行( )min,离灯塔B最近.
 的水塘外,准备把剩余的一半作为绿化用地.试求绿化用地的面积.
的水塘外,准备把剩余的一半作为绿化用地.试求绿化用地的面积. ,sin28°=0.4695,cos28°=0.8829,tan28°=0.5317)
,sin28°=0.4695,cos28°=0.8829,tan28°=0.5317)