题目内容

计算sin245°+cos30°•tan60°，其结果是（　　）
A、2
B、1
C、
5
2
D、
5
4
练习册系列答案
相关题目
如图，将△ABC沿DE翻折，DE∥BC，若
AD
BD
=
1
3
，BC=8，则DE的长为（　　）
A、2B、2.4C、3D、4
已知，如图，E（-4，2），F（-1，-1）以O为位似中心，按比例尺1：2把△EFO缩小，点E的对应点的坐标（　　）
A、（-2，1）B、（2，-1）C、（2，-1）或（-2，1）D、（-2，1）或（2，-1）
在Rt△ABC中，∠C=90°，AB=2BC，现给出下列结论：
①sinA=
3
2
；②cosB=
1
2
；③tanA=
3
3
；④tanB=
3
，
其中正确的有（　　）
A、①②③B、①②④
C、①③④D、②③④
在Rt△ABC中，∠C=90°，sinA=
5
13
，则tanB的值为（　　）
A、
12
13
B、
5
12
C、
13
12
D、
12
5
∠A是锐角，且sinA=cosA，则∠A的度数是（　　）
A、30°B、45°C、60°D、75°
2cos30°的值等于（　　）
A、
3
3
B、
3
C、
2
D、
3
2
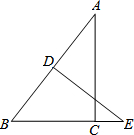如图，在Rt△ABC中，∠ACB=90°，BC=3，cosA=
4
5
，AB的垂直平分线DE交BC的延长线于点E，则DE的长为（　　）
A、
3
2
B、
10
3
C、
25
6
D、2
下列几何体的主视图是三角形的是（　　）
A、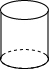B、C、D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网