题目内容
 某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
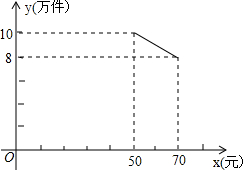
某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.(1)当50≤x≤70时,求出甲种产品的年销售量y(万元)与x(元)之间的函数关系式.
(2)若公司第一年的年销售量利润(年销售利润=年销售收入-生产成本)为W(万元),那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?
(3)第二年公司可重新对产品进行定价,在(2)的条件下,并要求甲种产品的销售单价x(元)在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利(总盈利=两年的年销售利润之和-投资成本)不低于85万元.请直接写出第二年乙种产品的销售单价m(元)的范围.
【答案】分析:(1)设y与x的函数关系式为y=kx+b(k≠0),然后把点(50,10),(70,8)代入求出k、b的值即可得解;
(2)先根据两种产品的销售单价之和为90元,根据乙种产品的定价范围列出不等式组求出x的取值范围是45≤x≤65,然后分45≤<50,50≤x≤65两种情况,根据销售利润等于两种产品的利润之和列出W与x的函数关系式,再利用二次函数的增减性确定出最大值,从而得解;
(3)用第一年的最大利润加上第二年的利润,然后根据总盈利不低于85万元列出不等式,整理后求解即可.
解答:解:(1)设y与x的函数关系式为y=kx+b(k≠0),
∵函数图象经过点(50,10),(70,8),
∴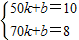 ,
,
解得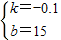 ,
,
所以,y=-0.1x+15;
(2)∵乙种产品的销售单价在25元(含)到45元(含)之间,
∴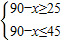 ,
,
解之得45≤x≤65,
①45≤x<50时,W=(x-30)(20-0.2x)+10(90-x-20),
=-0.2x2+16x+100,
=-0.2(x2-80x+1600)+320+100,
=-0.2(x-40)2+420,
∵-0.2<0,
∴x>40时,W随x的增大而减小,
∴当x=45时,W有最大值,W最大=-0.2(45-40)2+420=415万元;
②50≤x≤65时,W=(x-30)(-0.1x+15)+10(90-x-20),
=-0.1x2+8x+250,
=-0.1(x2-80x+1600)+160+250,
=-0.1(x-40)2+410,
∵-0.1<0,
∴x>40时,W随x的增大而减小,
∴当x=50时,W有最大值,W最大=-0.1(50-40)2+410=400万元.
综上所述,当x=45,即甲、乙两种产品定价均为45元时,第一年的年销售利润最大,最大年销售利润是415万元;
(3)根据题意得,W=-0.1x2+8x+250+415-700=-0.1x2+8x-35,
令W=85,则-0.1x2+8x-35=85,解得x1=20,x2=60.
又由题意知,50≤x≤65,根据函数性质分析,50≤x≤60,
即50≤90-m≤60,
∴30≤m≤40.
点评:本题考查了二次函数的性质在实际生活中的应用,最大销售利润的问题常利函数的增减性来解答,本题最大的特点就是要根据x的范围的不同分情况列出不同的函数关系式,其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x= 时取得.
时取得.
(2)先根据两种产品的销售单价之和为90元,根据乙种产品的定价范围列出不等式组求出x的取值范围是45≤x≤65,然后分45≤<50,50≤x≤65两种情况,根据销售利润等于两种产品的利润之和列出W与x的函数关系式,再利用二次函数的增减性确定出最大值,从而得解;
(3)用第一年的最大利润加上第二年的利润,然后根据总盈利不低于85万元列出不等式,整理后求解即可.
解答:解:(1)设y与x的函数关系式为y=kx+b(k≠0),
∵函数图象经过点(50,10),(70,8),
∴
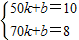 ,
,解得
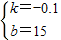 ,
,所以,y=-0.1x+15;
(2)∵乙种产品的销售单价在25元(含)到45元(含)之间,
∴
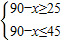 ,
,解之得45≤x≤65,
①45≤x<50时,W=(x-30)(20-0.2x)+10(90-x-20),
=-0.2x2+16x+100,
=-0.2(x2-80x+1600)+320+100,
=-0.2(x-40)2+420,
∵-0.2<0,
∴x>40时,W随x的增大而减小,
∴当x=45时,W有最大值,W最大=-0.2(45-40)2+420=415万元;
②50≤x≤65时,W=(x-30)(-0.1x+15)+10(90-x-20),
=-0.1x2+8x+250,
=-0.1(x2-80x+1600)+160+250,
=-0.1(x-40)2+410,
∵-0.1<0,
∴x>40时,W随x的增大而减小,
∴当x=50时,W有最大值,W最大=-0.1(50-40)2+410=400万元.
综上所述,当x=45,即甲、乙两种产品定价均为45元时,第一年的年销售利润最大,最大年销售利润是415万元;
(3)根据题意得,W=-0.1x2+8x+250+415-700=-0.1x2+8x-35,
令W=85,则-0.1x2+8x-35=85,解得x1=20,x2=60.
又由题意知,50≤x≤65,根据函数性质分析,50≤x≤60,
即50≤90-m≤60,
∴30≤m≤40.
点评:本题考查了二次函数的性质在实际生活中的应用,最大销售利润的问题常利函数的增减性来解答,本题最大的特点就是要根据x的范围的不同分情况列出不同的函数关系式,其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=
 时取得.
时取得. 
练习册系列答案
相关题目
 (2013•随州)某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
(2013•随州)某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.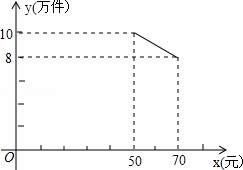
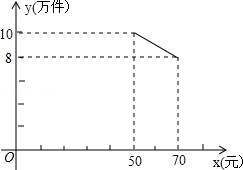
 某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
某公司投资700万元购甲、乙两种产品的生产技术和设备后,进行这两种产品加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价为x(元),年销售量为y(万件),当35≤x<50时,y与x之间的函数关系式为y=20-0.2x;当50≤x≤70时,y与x的函数关系式如图所示,乙种产品的销售单价,在25元(含)到45元(含)之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.