题目内容
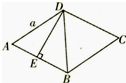 已知:菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a,
已知:菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a,(1)∠ABC的度数为
(2)对角线AC的长为
(3)菱形ABCD的面积为
分析:(1)根据已知可得到△ABD是等边三角形,从而得到∠ABD=60°,则可得到)∠ABC的度数;
(2)根据勾股定理可求得AC的长.
(3)根据菱形的面积等于两对角线乘积的一半可求得菱形的面积.
(2)根据勾股定理可求得AC的长.
(3)根据菱形的面积等于两对角线乘积的一半可求得菱形的面积.
解答:解:(1)根据已知条件和菱形的性质可得DE垂直且平分AB,所以△ABD是等边三角形,即∠ABD=60°,菱形的对角线平分一组对角,所以∠ABC的度数为2×60°=120°;
(2)由以上所求结果可得BD=AB=a,则(
)2=a2-
,即AC=
a;
(3)菱形ABCD的面积=
×a×
a=
a2.
(2)由以上所求结果可得BD=AB=a,则(
| AC |
| 2 |
| a2 |
| 4 |
| 3 |
(3)菱形ABCD的面积=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
点评:本题考查的是菱形的面积求法及菱形性质的综合.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
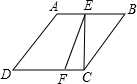 如图,已知,菱形ABCD中E是AB的中点,F是CD的四等分点,即CF:FD=1:3,则S四边形EBCF:S菱形ABCD=( )
如图,已知,菱形ABCD中E是AB的中点,F是CD的四等分点,即CF:FD=1:3,则S四边形EBCF:S菱形ABCD=( )| A、1:6 | B、2:7 | C、3:8 | D、5:12 |
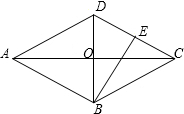 已知:菱形ABCD中,对角线AC=16cm,BD=12cm,BE⊥CD于点E,则BE的长为
已知:菱形ABCD中,对角线AC=16cm,BD=12cm,BE⊥CD于点E,则BE的长为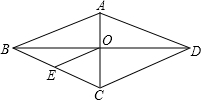 已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( ) 已知:菱形ABCD中,对角线AC=16cm,BD=12cm,DE⊥BC于点E,求菱形ABCD的面积和BE的长
已知:菱形ABCD中,对角线AC=16cm,BD=12cm,DE⊥BC于点E,求菱形ABCD的面积和BE的长