Question

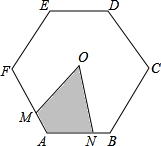正六边形的中心角∠MON （=60°）绕中心O旋转．试证：无论中心角旋转到何种位置，阴影部分的面积总等于这个正六边形面积的．

Answer 1

证明：连接OB、OA，
∵∠AOM+∠AON=60°，∠AON+∠NOB=60°，
∴∠AOM=∠NOB，
∵∠OAM+∠OAB=120°，∠OBA+∠OAB=120°，
∴∠OAM=∠OBN，
∵OA=OB，
∴△OAM≌△OBN（ASA），
∴S_阴影=S_△OAB=S_{六边形ABCDEF}．
分析：连接OB、OA，根据正多边形内角和定理求出∠OAM=∠OBN，再由全等三角形的判定定理即可得出△OAM≌△OBN即可得出结论．
点评：本题考查的是正多边形和圆，解答此题的关键是熟知正六边形的性质及全等三角形的判定定理．