题目内容
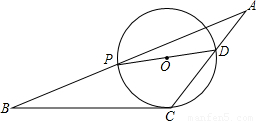
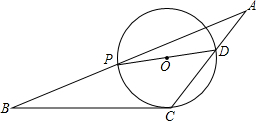 如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于
如图,已知,PD为⊙O的直径,直线BC切⊙O于点C,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于
- A.34°
- B.36°
- C.38°
- D.40°
B
分析:连接OC,根据直线BC切⊙O于点C,则可得∠OCB=90°,利用圆周角定理,三角形内角和与等边对等角可求得∠PDC=36°.
解答: 解:连接OC,
解:连接OC,
∵直线BC切⊙O于点C,
∴∠OCB=90,
∵∠A=28°,∠B=26°,
∴∠ACB=180°-∠B-∠A=126°,∠OCD=∠ACB-∠OCB=36°;
∵OC=OD,
∴∠PDC=∠OCD=36°.
故选B.
点评:本题主要考查了:①等边对等角;②切线的概念;③圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:连接OC,根据直线BC切⊙O于点C,则可得∠OCB=90°,利用圆周角定理,三角形内角和与等边对等角可求得∠PDC=36°.
解答:
 解:连接OC,
解:连接OC,∵直线BC切⊙O于点C,
∴∠OCB=90,
∵∠A=28°,∠B=26°,
∴∠ACB=180°-∠B-∠A=126°,∠OCD=∠ACB-∠OCB=36°;
∵OC=OD,
∴∠PDC=∠OCD=36°.
故选B.
点评:本题主要考查了:①等边对等角;②切线的概念;③圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 16、如图,已知,PD为⊙O的直径,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( )
16、如图,已知,PD为⊙O的直径,BP的延长线与CD的延长线交于点A,∠A=28°,∠B=26°,则∠PDC等于( )