题目内容
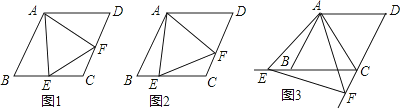
【题目】如图,已知△ABC和△CEF是两个不等的等边三角形,且有一个公共顶点C,连接AF和BE,线段AF和BE有怎样的大小关系?证明你的猜想. 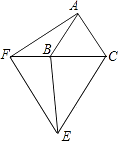
【答案】解:AF=BE.理由如下:
∵△ABC和△CEF是两个不等的等边三角形,
∴AC=BC,CE=CF,∠ACB=60°,∠ECF=60°,
在△ACF和△BCE中 ,
,
∴△ACF≌△BCE,
∴AF=BE.
【解析】先利用等边三角形的性质得到AC=BC,CE=CF,∠ACB=60°,∠ECF=60°,再利用“SAS”证明△ACF≌△BCE,然后根据全等三角形的性质得AF=BE.
【考点精析】掌握等边三角形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )

A. 这次被调查的学生人数为200人 B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选F的人数为35人 D. 被调查的学生中最想选D的有55人