Question

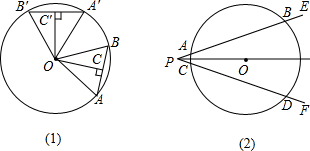
我们学习了“弧、弦、圆心角的关系”，实际上我们还可以得到“圆心角、弧、弦、弦心距之间的关系”如下：圆心角、弧、弦、弦心距之间的关系：在同圆或等圆中，如果两个圆心角i两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们对应的其余各组量也相等．（弦心距指从圆心到弦的距离（如图（1）中的OC、OC′），弦心距也可以说成圆心到弦的垂线段的长度．）
请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题．
如图（2），O是∠EPF的平分线上一点，以点O为圆心的圆与角的两边分别交子点A、B、C、D．
（1）求证：AB=CD；
（2）若角的顶点P在圆上或圆内，上述结论还成立吗？若不成立，请说明理由；若成立，请加以证明．

Answer 1

（1）证明：如图1，过O作OM⊥AB于M，ON⊥CD于N，
则∠OMB=∠OND=90°，
∵PO平分∠EPF，
∴OM=ON，
在Rt△OMB和Rt△OND中

∴Rt△OMB≌Rt△OND（HL），
∴BM=DN，
∵OM⊥AB，ON⊥CD，OM、ON过O，
∴AB=2BM，CD=2DN，
∴AB=CD；
（2）还成立，
证明：如图2，当P在⊙O上时，
∵由（1）知：BM=DN，AB=2BM，CD=2DN，
∴AB=CD；
当P在⊙O内时，如图3，
∵由（1）知：BM=DN，AB=2BM，CD=2DN，
∴AB=CD．
分析：（1）过O作OM⊥AB于M，ON⊥CD于N，求出ON=OM，证△OMB≌△OND，推出BM=DN，根据垂径定理得出AB=2BM，CD=2DN，即可得出答案；
（2）过O作OM⊥AB于M，ON⊥CD于N，求出ON=OM，证△OMB≌△OND，推出BM=DN，根据垂径定理得出AB=2BM，CD=2DN，即可得出答案．
点评：本题考查了垂径定理，角平分线性质，全等三角形的性质和判定的应用，主要考查学生运用定理进行推理的能力，题目比较好，证明过程类似．