题目内容
 如图AC⊥BC,BD⊥AD,AC=BD,则图中全等三角形的对数为____对.
如图AC⊥BC,BD⊥AD,AC=BD,则图中全等三角形的对数为____对.
- A.0
- B.1
- C.2
- D.3
C
分析:根据垂直定义求出∠C=∠D=90°,根据HL证Rt△ACB≌Rt△BDA,推出∠DAB=∠CBA,BC=AD,根据等腰三角形性质求出C=OD,根据SAS证△ACO≌△BDO即可.
解答:有2对,是△ACB≌△BDA,△ACO≌△BDO,
理由是:∵AC⊥BC,AD⊥BD,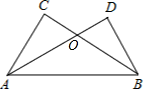
∴∠C=∠D=90°,
在Rt△ACB和Rt△BDA中
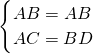 ,
,
∴Rt△ACB≌Rt△BDA,
∴∠DAB=∠CBA,BC=AD,
∴OA=OB,
∴OC=OD,
在△ACO和△BDO中
 ,
,
∴△ACO≌△BDO.
故选C.
点评:本题考查了等腰三角形的性质,垂直,全等三角形的性质和判定等知识点的运用,能熟练地运用定理进行推理是解此题的关键,培养了学生分析问题和解决问题的能力.
分析:根据垂直定义求出∠C=∠D=90°,根据HL证Rt△ACB≌Rt△BDA,推出∠DAB=∠CBA,BC=AD,根据等腰三角形性质求出C=OD,根据SAS证△ACO≌△BDO即可.
解答:有2对,是△ACB≌△BDA,△ACO≌△BDO,
理由是:∵AC⊥BC,AD⊥BD,

∴∠C=∠D=90°,
在Rt△ACB和Rt△BDA中
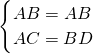 ,
,∴Rt△ACB≌Rt△BDA,
∴∠DAB=∠CBA,BC=AD,
∴OA=OB,
∴OC=OD,
在△ACO和△BDO中
 ,
,∴△ACO≌△BDO.
故选C.
点评:本题考查了等腰三角形的性质,垂直,全等三角形的性质和判定等知识点的运用,能熟练地运用定理进行推理是解此题的关键,培养了学生分析问题和解决问题的能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 如图AC⊥BC,BD⊥AD,AC=BD,则图中全等三角形的对数为( )对.
如图AC⊥BC,BD⊥AD,AC=BD,则图中全等三角形的对数为( )对.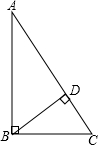 如图AB⊥BC,BD⊥AC,能表示点A到BC距离的线段共有( )
如图AB⊥BC,BD⊥AC,能表示点A到BC距离的线段共有( )
