题目内容
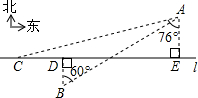 如图,在一条东西公路l的两侧分别有村庄A和B,村庄A到公路的距离为3km,村庄A位于村庄B北偏东60°的方向,且与村庄B相距10km.现有一辆长途客车从位于村庄A南偏西76°方向的C处,正沿公路l由西向东以40km/h的速度行驶,此时,小明正以25km/h的速度由B村出发,向正北方向赶往公路l的D处搭乘这趟客车.
如图,在一条东西公路l的两侧分别有村庄A和B,村庄A到公路的距离为3km,村庄A位于村庄B北偏东60°的方向,且与村庄B相距10km.现有一辆长途客车从位于村庄A南偏西76°方向的C处,正沿公路l由西向东以40km/h的速度行驶,此时,小明正以25km/h的速度由B村出发,向正北方向赶往公路l的D处搭乘这趟客车.
(1)求村庄B到公路l的距离;
(2)小明能否搭乘上这趟长途客车?
(参考数据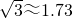 ,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
 解:(1)设AB与l交于点O.
解:(1)设AB与l交于点O.在Rt△AOE中,
∵∠OAE=60°,AE=3,
∴OA=
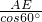 =6,
=6,∵AB=10,
∴OB=AB-OA=4.
在Rt△BOD中,∠OBD=∠OAE=60°,
∴BD=OB•cos60°=2.
∴观测点B到公路l的距离为2km;
(2)能.
CD=3tan76°-5
 ≈3.38.
≈3.38.t客车=
 =0.0845(h),t小明=
=0.0845(h),t小明=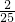 =0.08(h),t客车>t小明.
=0.08(h),t客车>t小明.分析:(1)将观测点B到航线l的距离用辅助线BD表示出来,要求BD,先求出OA,OB,再在Rt△OBD中,求出BD即可.
(2)先根据题意求出CD的长度,然后分别表示出客车用的时间及小明用的时间,继而可判断出答案.
点评:本题考查解直角三角形的应用,难度一般,解答此题的关键是构造出直角三角形,利用直角三角形的性质解答.

练习册系列答案
相关题目
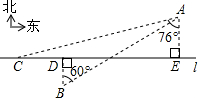 如图,在一条东西公路l的两侧分别有村庄A和B,村庄A到公路的距离为3km,村庄A位于村庄B北偏东60°的方向,且与村庄B相距10km.现有一辆长途客车从位于村庄A南偏西76°方向的C处,正沿公路l由西向东以40km/h的速度行驶,此时,小明正以25km/h的速度由B村出发,向正北方向赶往公路l的D处搭乘这趟客车.
如图,在一条东西公路l的两侧分别有村庄A和B,村庄A到公路的距离为3km,村庄A位于村庄B北偏东60°的方向,且与村庄B相距10km.现有一辆长途客车从位于村庄A南偏西76°方向的C处,正沿公路l由西向东以40km/h的速度行驶,此时,小明正以25km/h的速度由B村出发,向正北方向赶往公路l的D处搭乘这趟客车.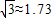 ,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)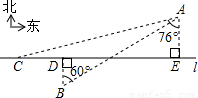
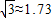 ,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)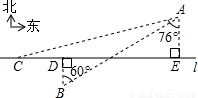
 ,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
,sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)