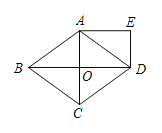
题目内容
【题目】如图,平行四边形![]() 的顶点
的顶点![]() 、
、![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,已知
轴上,已知![]() ,
,![]() ,
,![]() .
.

(1)平行四边形![]() 的面积为________;
的面积为________;
(2)如图1,点![]() 是
是![]() 边上的一点,若
边上的一点,若![]() 的面积是平行四边形
的面积是平行四边形![]() 的
的![]() ,求点
,求点![]() 的坐标;
的坐标;
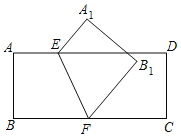
(3)如图2,将![]() 绕点
绕点![]() 顺时针旋转,旋转得
顺时针旋转,旋转得![]() ,在整个旋转过程中,能否使以点
,在整个旋转过程中,能否使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若能,求点
为顶点的四边形是平行四边形?若能,求点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)32;(2)点E的坐标为(![]() ,2);(3)能,点A1的坐标为
,2);(3)能,点A1的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由题意可得AB=8,根据平行四边形的面积公式可求得ABCD的面积;
(2)过点E作EF⊥AB,根据△ABE的面积是ABCD的![]() ,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
,可求EF的长,根据B点,C点坐标可求直线BC的解析式,把点E的纵坐标代入可求点E的坐标;
(3)分以下三种情况讨论:①四边形OA1D1B是平行四边形,②四边形A1D1OB是平行四边形,③四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E.先分别画出示意图,利用旋转的性质,平行四边形的性质再结合面积法及勾股定理可分别得出点A1的坐标.
解:(1)∵OA=3,OB=5,OD=4.
∴AB=8,∴ABCD的面积=4×8=32,
故答案为:32;
(2)过点E作EF⊥AB于F,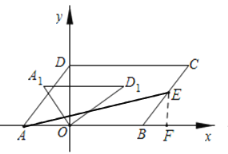
∵S△ABE=![]() SABCD,∴
SABCD,∴![]() ×AB×EF=
×AB×EF=![]() ×32,∴EF=2.
×32,∴EF=2.
∵OB=5,CD=AB=8,OD=4,
∴点B(5,0),点C(8,4),
设直线BC的解析式为y=kx+b,
![]() ,解得
,解得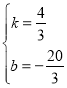 ,
,
∴直线BC的解析式为y=![]() ,
,
当y=2时,x=![]() ,
,
∴点E的坐标为(![]() ,2);
,2);
(3)能使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,理由如下:
为顶点的四边形是平行四边形,理由如下:
∵OA=3,OD=4,∴AD=5,分以下三种情况:
①如图,若四边形OA1D1B是平行四边形,A1D1交y轴于点F,
∵将△AOD绕点O顺时针旋转,旋转得△A1OD1,
∴A1O=AO=3,OD1=OD=4,∠A1OD1=∠AOD=90°.
∵四边形OA1D1B是平行四边形,
∴A1D1=BO=5,A1D1∥AB,∴∠A1FO=180°-∠AOD=90°,
∴S△A1OD1=![]() ×A1O×OD1=
×A1O×OD1=![]() ×A1D1×OF,
×A1D1×OF,
∴OF=![]() ,
,![]() ,
,
∵点A1在第二象限,∴A1的坐标为![]() ;
;
②如图,若四边形A1D1OB是平行四边形,A1D1交y轴于点F,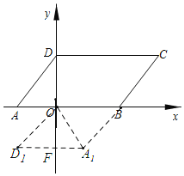
同①可得,![]() ,
,
∵点A1在第四象限,∴A1的坐标为![]() ;
;
③如图,若四边形OA1BD1是平行四边形,过点A1作A1E⊥BA于点E,
∵OA1BD1是平行四边形,且∠A1OD1=90°,
∴四边形OA1BD1是矩形,∴OD1=A1B=4,∠OA1B=90°,
∵S△A1OB=![]() ×OB×A1E=
×OB×A1E=![]() ×A1O×A1B,
×A1O×A1B,
∴A1E=![]() ,∴OE=
,∴OE=![]() ,
,
∴A1的坐标为![]() .
.
综上所述,符合条件的点A1的坐标为![]() 或
或![]() 或
或![]() .
.