题目内容
某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.
活动一:
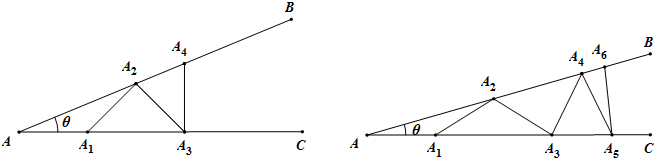
如图甲所示,从点A1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答:
(2)设AA1=A1A2=A2A3=1.
①θ=
②若记小棒A2n-1A2n的长度为an(n为正整数,如A1A2=a1,A3A4=a2,…),求出此时a2,a3的值,并直接写出an(用含n的式子表示).
活动二:
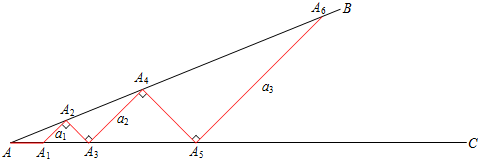
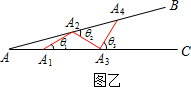
如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经向右摆放了3根小棒,则θ1=
(4)若只能摆放4根小棒,求θ的范围.
分析:(1)本题需先根据已知条件∠BAC=θ(0°<θ<90°)小棒两端分别落在两射线上,从而判断出能继续摆下去.
(2)本题需先根据已知条件AA1=A1A2=A2A3=1,A1A2⊥A2A3,得出A2A3和AA3的值,判断出A1A2∥A3A4、A3A4∥A5A6,即可求出∠A=∠AA2A1=∠AA4A3=∠AA6A,从而此时a2,a3的值和出an.
(3)本题需先根据A1A2=AA1,得出∠A1AA2和∠AA2A1相等,即可得出θ1的值,同样道理得出θ2、θ3的值.
(4)本题需先根据已知条件,列出不等式,解出θ的取值范围,即可得出正确答案.
(2)本题需先根据已知条件AA1=A1A2=A2A3=1,A1A2⊥A2A3,得出A2A3和AA3的值,判断出A1A2∥A3A4、A3A4∥A5A6,即可求出∠A=∠AA2A1=∠AA4A3=∠AA6A,从而此时a2,a3的值和出an.
(3)本题需先根据A1A2=AA1,得出∠A1AA2和∠AA2A1相等,即可得出θ1的值,同样道理得出θ2、θ3的值.
(4)本题需先根据已知条件,列出不等式,解出θ的取值范围,即可得出正确答案.
解答:解:(1)∵根据已知条件∠BAC=θ(0°<θ<90°)小棒两端能分别落在两射线上,
∴小棒能继续摆下去.
故答案为:能;
(2)①∵A1A2=A2A3,A1A2⊥A2A3,
∴∠A2A1A3=45°,
∴∠AA2A1+∠θ=45°,
∵∠AA2A1=∠θ,
∴∠θ=22.5°;
②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3
∴A1A3=
,AA3=1+
又∵A2A3⊥A3A4
A1A2∥A3A4
同理;A3A4∥A5A6
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+
a3=AA3+A3A5=a2+A3A5
∵A3A5=
a2,
∴a3=A5A6=AA5=a2+
a2=(
+1)2
∴an=(
+1)n-1;
(3)∵A1A2=AA1
∴∠A1AA2=∠AA2A1=θ
∴∠A2A1A3=θ1=θ+θ
∴θ1=2θ
同理可得:θ2=3θ
θ3=4θ;
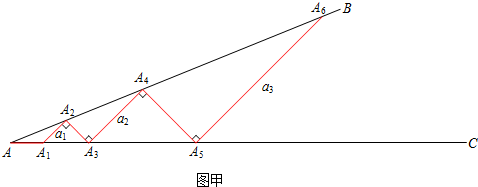
(4)如图:
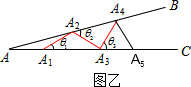
∵A4A3=A4A5,
∴∠A4A3A5=∠A4A5A3=4θ°,
∵根据三角形内角和定理和等腰三角形的性质,
当∠A5A4B是钝角或直角时,不能继续摆放小棒了,
∴当∠A4A3A5是锐角,∠A5A4B=5θ是钝角或直角时,只能摆放4根小棒,
∴5θ≥90°,4θ<90°,
即
,
∴18°≤θ<22.5°.
故答案为:能,22.5°,2θ,3θ,4θ.
∴小棒能继续摆下去.
故答案为:能;
(2)①∵A1A2=A2A3,A1A2⊥A2A3,
∴∠A2A1A3=45°,
∴∠AA2A1+∠θ=45°,
∵∠AA2A1=∠θ,
∴∠θ=22.5°;
②∵AA1=A1A2=A2A3=1,A1A2⊥A2A3
∴A1A3=
| 2 |
| 2 |
又∵A2A3⊥A3A4
A1A2∥A3A4
同理;A3A4∥A5A6
∴∠A=∠AA2A1=∠AA4A3=∠AA6A5
∴AA3=A3A4,AA5=A5A6
∴a2=A3A4=AA3=1+
| 2 |
a3=AA3+A3A5=a2+A3A5
∵A3A5=
| 2 |
∴a3=A5A6=AA5=a2+
| 2 |
| 2 |
∴an=(
| 2 |
(3)∵A1A2=AA1
∴∠A1AA2=∠AA2A1=θ
∴∠A2A1A3=θ1=θ+θ
∴θ1=2θ
同理可得:θ2=3θ
θ3=4θ;
(4)如图:

∵A4A3=A4A5,
∴∠A4A3A5=∠A4A5A3=4θ°,
∵根据三角形内角和定理和等腰三角形的性质,
当∠A5A4B是钝角或直角时,不能继续摆放小棒了,
∴当∠A4A3A5是锐角,∠A5A4B=5θ是钝角或直角时,只能摆放4根小棒,
∴5θ≥90°,4θ<90°,
即
|
∴18°≤θ<22.5°.
故答案为:能,22.5°,2θ,3θ,4θ.
点评:本题主要考查了相似三角形的判定和性质,在解题时要注意根据题意找出规律并与相似三角形的性质相结合是本题的关键.

练习册系列答案
相关题目