题目内容
 某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540米2,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图(1)、图(2)中道路的宽分别是多少?
某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540米2,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图(1)、图(2)中道路的宽分别是多少?
解:(1)设道路的宽为x米.依题意得:
(32-2x)(20-2x)=540,
整理得出:x2-26x+25=0,
即(x-1)(x-25)=0,
解之得x1=1,x2=25(不合题意舍去).
答:道路宽为1m.
(2)设道路的宽为x米.依题意得:
(32-x)(20-x)=540,
整理得出:x2-52x+100=0,
即(x-2)(x-50)=0,
解之得x1=2,x2=50(不合题意舍去).
答:道路宽为2m.
分析:(1)设道路的宽为x米.长应该为32-2x,宽应该为20-2x;那么根据耕地的面积为540m2,即可得出方程,求解即可.
(2)如果设路宽为xm,耕地的长应该为32-x,宽应该为20-x;那么根据耕地的面积为540m2,即可得出方程,求解即可.
点评:本题考查一元二次方程的应用,难度中等.可将耕地面积看作一整块的矩形的面积,根据矩形面积=长×宽求解.
(32-2x)(20-2x)=540,
整理得出:x2-26x+25=0,
即(x-1)(x-25)=0,
解之得x1=1,x2=25(不合题意舍去).
答:道路宽为1m.
(2)设道路的宽为x米.依题意得:
(32-x)(20-x)=540,
整理得出:x2-52x+100=0,
即(x-2)(x-50)=0,
解之得x1=2,x2=50(不合题意舍去).
答:道路宽为2m.
分析:(1)设道路的宽为x米.长应该为32-2x,宽应该为20-2x;那么根据耕地的面积为540m2,即可得出方程,求解即可.
(2)如果设路宽为xm,耕地的长应该为32-x,宽应该为20-x;那么根据耕地的面积为540m2,即可得出方程,求解即可.
点评:本题考查一元二次方程的应用,难度中等.可将耕地面积看作一整块的矩形的面积,根据矩形面积=长×宽求解.

练习册系列答案
相关题目
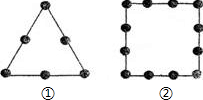 为了迎接校23届艺术节,校艺术社团同学为了美化校园,准备在校园一角设计一个正n边形图案,计划在每边上摆放n盘花进行装饰.已知每盘花按
为了迎接校23届艺术节,校艺术社团同学为了美化校园,准备在校园一角设计一个正n边形图案,计划在每边上摆放n盘花进行装饰.已知每盘花按 某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540米2,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图(1)、图(2)中道路的宽分别是多少?
某校为了美化校园,准备在一块长32米、宽20米的长方形场地上修筑若干条等宽道路,余下部分作草坪,使草坪面积为540米2,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),请你根据两种设计方案各列出方程,求图(1)、图(2)中道路的宽分别是多少? 某学校为了美化校园,准备在长40米,款30米的矩形空地内种植花草,中间留有几条等宽的小道,若要保证花草种植面积达到100平方米,小道的宽应为多少米?设小道宽为x米,则可列方程( )
某学校为了美化校园,准备在长40米,款30米的矩形空地内种植花草,中间留有几条等宽的小道,若要保证花草种植面积达到100平方米,小道的宽应为多少米?设小道宽为x米,则可列方程( )