题目内容
【题目】在⊙O中,AB为直径,C为⊙O上一点.

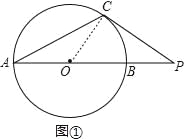
(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
【答案】(1)∠P =36°;(2)∠P=30°.
【解析】
试题(Ⅰ)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答案;
(Ⅱ)根据E为AC的中点得到OD⊥AC,从而求得∠AOE=90°﹣∠EAO=80°,然后利用圆周角定理求得∠ACD=![]() ∠AOD=40°,最后利用三角形的外角的性质求解即可.
∠AOD=40°,最后利用三角形的外角的性质求解即可.
试题解析:(Ⅰ)如图,连接OC,
∵⊙O与PC相切于点C,
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°﹣∠COP=36°;
(Ⅱ)∵E为AC的中点,
∴OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°﹣∠EAO=80°,
∴∠ACD=![]() ∠AOD=40°,
∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD﹣∠A=40°﹣10°=30°.

【题目】为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣30 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)若购进乙种运动鞋x(双),要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于13000元且不超过13500元,问该专卖店有几种进货方案;
(3)在(2)的条件下求出总利润y(元)与购进乙种运动鞋x(双)的函数关系式,并用关系式说明哪种方案的利润最大,最大利润是多少.



