题目内容
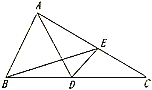
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.

(1)若AB=AC=10cm,BC=6cm,求△BCE的周长;
(2)若∠A=40°,求∠EBC的度数.
【答案】(1)16cm;(2)30°.
【解析】
(1)已知DE垂直平分AB,根据线段垂直平分线的性质可得EA=EB,再由△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC即可求得△BCE的周长;(2)已知AB=AC,∠A=40°,根据等腰三角形的性质及三角形的内角和定理可得∠ABC=∠C=70°,再由EA=EB,∠A=40°,根据等腰三角形的性质可得∠A=∠ABE=40°;由∠EBC=∠ABC-∠ABE即可求得∠EBC的度数.
(1)∵DE垂直平分AB,
∴EA=EB,
∵AB=AC=10cm,BC=6cm,
∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=10cm+6cm=16cm.
(2)∵AB=AC,∠A=40°,
∴∠ABC=∠C=70°,
∵EA=EB,∠A=40°,
∴∠A=∠ABE=40°,
∴∠EBC=∠ABC-∠ABE=70°-40°=30°.

练习册系列答案
相关题目