题目内容
双曲线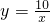 与
与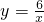 在第一象限内的图象依次是M和N,设点P在图象M上,PC垂直于x轴于点C交图象N于点A.PD垂直于y轴于D点,交图象N于点B,则四边形PAOB的面积为
在第一象限内的图象依次是M和N,设点P在图象M上,PC垂直于x轴于点C交图象N于点A.PD垂直于y轴于D点,交图象N于点B,则四边形PAOB的面积为
- A.8
- B.6
- C.4
- D.2
C
分析:由双曲线上点的性质可知,点P在双曲线M上,故S矩形OCPD=OC×PC=xy=10,点A、B在双曲线N上,故S△OAC=S△OBD= ×OC×AC=
×OC×AC= xy=3,根据S四边形PAOB-S矩形OCPD-S△OAC=S△OBD求面积.
xy=3,根据S四边形PAOB-S矩形OCPD-S△OAC=S△OBD求面积.
解答: 解:∵点P在双曲线M上,
解:∵点P在双曲线M上,
∴S矩形OCPD=OC×PC=xy=10,
又∵点A、B在双曲线N上,
∴S△OAC=S△OBD= ×OC×AC=
×OC×AC= xy=3,
xy=3,
∴S四边形PAOB-S矩形OCPD-S△OAC=S△OBD=10-3-3=4.
故选C.
点评:本题考查了双曲线上点的坐标与图形面积的关系.过双曲线y= 上一点作x轴、y轴的垂线,所围成的矩形面积为|k|,所围成的三角形面积为
上一点作x轴、y轴的垂线,所围成的矩形面积为|k|,所围成的三角形面积为 |k|.
|k|.
分析:由双曲线上点的性质可知,点P在双曲线M上,故S矩形OCPD=OC×PC=xy=10,点A、B在双曲线N上,故S△OAC=S△OBD=
 ×OC×AC=
×OC×AC= xy=3,根据S四边形PAOB-S矩形OCPD-S△OAC=S△OBD求面积.
xy=3,根据S四边形PAOB-S矩形OCPD-S△OAC=S△OBD求面积.解答:
 解:∵点P在双曲线M上,
解:∵点P在双曲线M上,∴S矩形OCPD=OC×PC=xy=10,
又∵点A、B在双曲线N上,
∴S△OAC=S△OBD=
 ×OC×AC=
×OC×AC= xy=3,
xy=3,∴S四边形PAOB-S矩形OCPD-S△OAC=S△OBD=10-3-3=4.
故选C.
点评:本题考查了双曲线上点的坐标与图形面积的关系.过双曲线y=
 上一点作x轴、y轴的垂线,所围成的矩形面积为|k|,所围成的三角形面积为
上一点作x轴、y轴的垂线,所围成的矩形面积为|k|,所围成的三角形面积为 |k|.
|k|. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
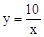 与
与 在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )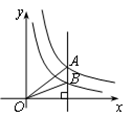
 与
与 在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
在第一象限内的图象如图所示,作一条平行于y轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )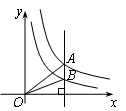
 与
与 在第一象限内的图象如图所示,作一条平行于y轴
在第一象限内的图象如图所示,作一条平行于y轴
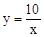 与
与 在第一象限内的图象如图所示,作
在第一象限内的图象如图所示,作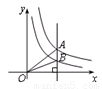
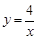 与
与 在第一象限内的图象如图所示,作一条平行于y轴
在第一象限内的图象如图所示,作一条平行于y轴