题目内容
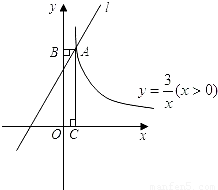
(2008•达州)平行于直线y=x的直线l不经过第四象限,且与函数y=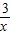 (x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.
(x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.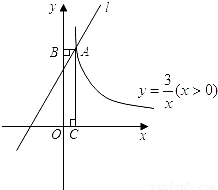
【答案】分析:设A点的坐标为(x,y),四边形ABOC的周长为8,可以得到2x+2y=8,则A的坐标为(x,4-x),把A点代入y=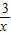 ,就得到关于x的方程,求出x的值.根据直线l平行与直线y=x,则一次项系数相同,因而可以设定直线l的解析式为y=x+b(b≥0),把A点的坐标代入就可以求出b的值,得到函数解析式.
,就得到关于x的方程,求出x的值.根据直线l平行与直线y=x,则一次项系数相同,因而可以设定直线l的解析式为y=x+b(b≥0),把A点的坐标代入就可以求出b的值,得到函数解析式.
解答:解:设A点的坐标为(x,y),
由题意得2x+2y=8,
整理得y=4-x,
即A的坐标为(x,4-x),
把A点代入y=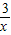 (x>0)中,
(x>0)中,
解得x=1或x=3,
∴A点的坐标是(1,3)或(3,1),
又由题意可设定直线l的解析式为y=x+b(b≥0),
把(1,3)点代入y=x+b,解得b=2;
把(3,1)点代入y=x+b,解得b=-2,不合要求,舍去.
所以直线l的解析式为y=x+2.
点评:本题考查了反比例函数的综合应用,关键是一次函数的图象平行的条件,即一次项系数相同.
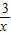 ,就得到关于x的方程,求出x的值.根据直线l平行与直线y=x,则一次项系数相同,因而可以设定直线l的解析式为y=x+b(b≥0),把A点的坐标代入就可以求出b的值,得到函数解析式.
,就得到关于x的方程,求出x的值.根据直线l平行与直线y=x,则一次项系数相同,因而可以设定直线l的解析式为y=x+b(b≥0),把A点的坐标代入就可以求出b的值,得到函数解析式.解答:解:设A点的坐标为(x,y),
由题意得2x+2y=8,
整理得y=4-x,
即A的坐标为(x,4-x),
把A点代入y=
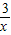 (x>0)中,
(x>0)中,解得x=1或x=3,
∴A点的坐标是(1,3)或(3,1),
又由题意可设定直线l的解析式为y=x+b(b≥0),
把(1,3)点代入y=x+b,解得b=2;
把(3,1)点代入y=x+b,解得b=-2,不合要求,舍去.
所以直线l的解析式为y=x+2.
点评:本题考查了反比例函数的综合应用,关键是一次函数的图象平行的条件,即一次项系数相同.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
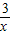 (x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.
(x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.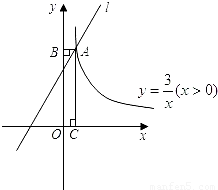
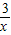 (x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.
(x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.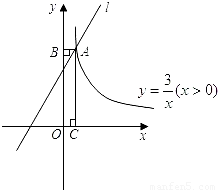
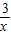 (x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.
(x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.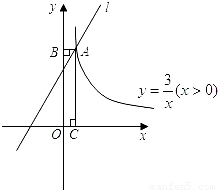
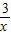 (x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.
(x>0)和图象交于点A,过点A作AB⊥y轴于点B,AC⊥x轴于点C,四边形ABOC的周长为8.求直线l的解析式.