Question

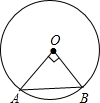
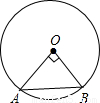
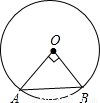
如图，⊙O中的圆心角∠AOB=90°，点O到弦AB的距离为4，则⊙O的直径长为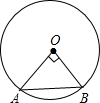

 

．

Answer 1

分析：过点O作OC⊥AB，垂足为C，可得AC=4，再由勾股定理得圆的半径，从而得出直径．

解答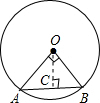：解：如图，过点O作OC⊥AB，垂足为C，
∵∠AOB=90°，∠A=∠AOC=45°，
∴OC=AC，
∵CO=4，
∴AC=4，
∴OA=

AC2+CO2

=4

2

，
∴⊙O的直径长为8

2

．
故答案为：8

2

．

点评：本题考查了勾股定理和等腰三角形的判定，是基础知识要熟练掌握．