题目内容
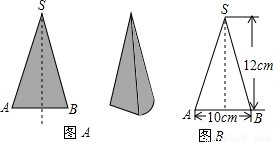
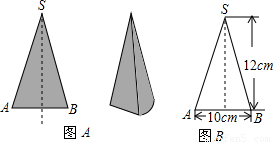
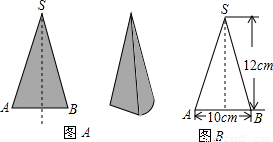
如图A,是一个圆锥形零件,经过轴的剖面是一个等腰三角形(如图B),则这个零件的表面积是( )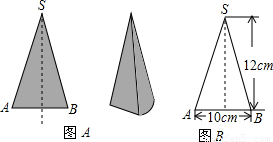
A.65πcm2
B.35πcm2
C.90πcm2
D.60πcm2
【答案】分析:根据圆面积公式,求得圆锥的底面积是25π;要计算圆锥的侧面积,首先根据勾股定理计算其母线长是
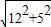 =13,再根据圆锥的侧面积公式得:圆锥的侧面积=
=13,再根据圆锥的侧面积公式得:圆锥的侧面积= ×底面周长×高=65π;所以圆锥的全面积是65π+25π=90π.
×底面周长×高=65π;所以圆锥的全面积是65π+25π=90π.
解答:解:根据圆面积公式,得:圆锥的底面积是25πcm2,
由勾股定理知,母线= =13cm,
=13cm,
圆锥的侧面积= ×底面周长×高=65πcm2,
×底面周长×高=65πcm2,
∴圆锥的全面积=65π+25π=90πcm2.
故选C.
点评:掌握圆锥的侧面积计算公式,熟练运用勾股定理表示圆锥的高、母线、底面半径三者之间的关系.
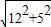 =13,再根据圆锥的侧面积公式得:圆锥的侧面积=
=13,再根据圆锥的侧面积公式得:圆锥的侧面积= ×底面周长×高=65π;所以圆锥的全面积是65π+25π=90π.
×底面周长×高=65π;所以圆锥的全面积是65π+25π=90π.解答:解:根据圆面积公式,得:圆锥的底面积是25πcm2,
由勾股定理知,母线=
 =13cm,
=13cm,圆锥的侧面积=
 ×底面周长×高=65πcm2,
×底面周长×高=65πcm2,∴圆锥的全面积=65π+25π=90πcm2.
故选C.
点评:掌握圆锥的侧面积计算公式,熟练运用勾股定理表示圆锥的高、母线、底面半径三者之间的关系.

练习册系列答案
相关题目
如图A,是一个圆锥形零件,经过轴的剖面是一个等腰三角形(如图B),则这个零件的表面积是( )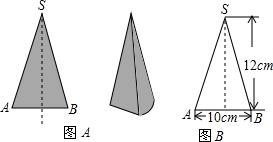

| A、65πcm2 | B、35πcm2 | C、90πcm2 | D、60πcm2 |