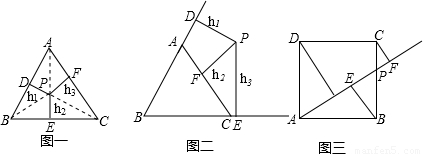
题目内容
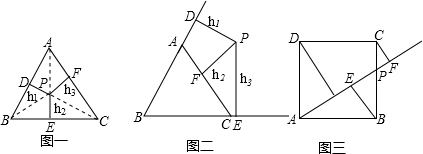
如图一，已知点P是边长为a的等边△ABC内任意一点，点P到三边的距离PD、PE、PF的长分别记为h1，h2，h3，则h1，h2，h3之间有什么关系呢？分析：连接PA、PB、PC，则△ABC被分割成三个三角形，根据：
S△PAB+S△PBC+S△PAC=S△ABC，即：
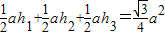，可得
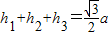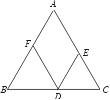
．问题1：若点P是边长为a的等边△ABC外一点（如图二所示位置），点P到三边的距离PD、PE、PF的长分别记为h1，h2，h3．探索h1，h2，h3之间有什么关系呢？并证明你的结论；
问题2：如图三，正方形ABCD的边长为a，点P是BC边上任意一点（可与B、C重合），B、C、D三点到射线AP的距离分别是h1，h2，h3，设h1+h2+h3=y，线段AP=x，求y与x的函数关系式，并求y的最大值与最小值．
【答案】分析：（1）探索h1，h2，h3之间的关系，可以根据等量关系S四边形ABCP=S△APC+S△ABC得出等式，解决问题；
（2）连接DP、AC，可知S四边形ABCP=S△APB+S△ADP+S△DCP，∵S△DCP=S△ACP，即S四边形ABCP=S△APB+S△ADP+S△ACP的等量关系，列出方程，得到y与x的函数关系式，按照自变量的取值范围求出y的最大值与最小值．
解答：解：问题1：h1+h2-h3=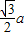
（2分）
理由：连接PA、PB、PC
∵PE⊥BC，PD⊥BA，且△ABC是边长为a的等边三角形
∴S△PAB=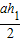
，S△PBC=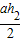
∴S四边形ABCP=S△PAB+S△PBC=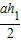
+
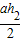（2分）
又∵S四边形ABCP=S△APC+S△ABC=
（1分）
∴
+
=
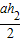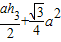即：h1+h2-h3=
；（1分）
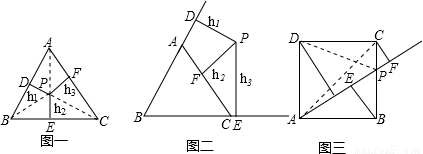
问题2：连接DP、AC
易求：S△APB+S△ADP+S△ACP=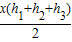
（2分）
易证：S△DCP=S△ACP（同底等高）（2分）
而S正方形ABCD=S△APB+S△ADP+S△DCP
∴
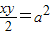
∴y=
（a≤x≤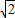
a）（2分）
∵2a2＞0
∴y随x的增大而减少
∴当x=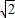
a时，y最小=
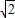a，当x=a时，y最大=2a．（2分）
点评：此题是一个综合性很强的题目，主要考查等边三角形的性质、解反比例函数等知识．难度较大，有利于培养同学们钻研和探索问题的精神．
（2）连接DP、AC，可知S四边形ABCP=S△APB+S△ADP+S△DCP，∵S△DCP=S△ACP，即S四边形ABCP=S△APB+S△ADP+S△ACP的等量关系，列出方程，得到y与x的函数关系式，按照自变量的取值范围求出y的最大值与最小值．
解答：解：问题1：h1+h2-h3=
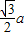（2分）理由：连接PA、PB、PC
∵PE⊥BC，PD⊥BA，且△ABC是边长为a的等边三角形
∴S△PAB=
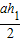，S△PBC=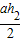∴S四边形ABCP=S△PAB+S△PBC=
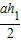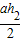+（2分）又∵S四边形ABCP=S△APC+S△ABC=
（1分）∴
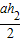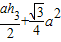+=即：h1+h2-h3=；（1分）问题2：连接DP、AC
易求：S△APB+S△ADP+S△ACP=
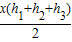（2分）易证：S△DCP=S△ACP（同底等高）（2分）
而S正方形ABCD=S△APB+S△ADP+S△DCP
∴
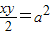
∴y=
（a≤x≤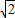a）（2分）∵2a2＞0
∴y随x的增大而减少
∴当x=
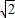a时，y最小=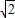a，当x=a时，y最大=2a．（2分）点评：此题是一个综合性很强的题目，主要考查等边三角形的性质、解反比例函数等知识．难度较大，有利于培养同学们钻研和探索问题的精神．
练习册系列答案
相关题目
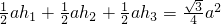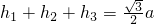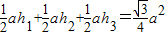，可得
．
，可得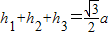
．