题目内容
如图，点O在△ABC的内部，∠A=40°，以下两题任选一题解答：
（1）若点O是△ABC的外心，则∠BOC的度数等于______；
（2）若点O是△ABC的内心，则∠BOC的度数等于______．
解：（1）若点O是△ABC的外心，则∠BOC=2∠BAC=2×40°=80°．故填80°．
（2）若点O是△ABC的内心，则∠BOC=90°+
∠BAC=90°+20°=110°．故填110°．
分析：（1）若点O为△ABC的外心，则∠BOC和∠BAC是同弧所对的圆心角和圆周角，利用圆周角定理可求出∠BOC．
（2）若点O为△ABC的内心，利用结论∠BOC=90°+∠BAC可计算出∠BOC．
点评：理解三角形外心和内心的定义，熟悉圆周角定理，记住三角形两内角的平分线的夹角等于90度与第三个角一半的和，是解决本题的关键．
（2）若点O是△ABC的内心，则∠BOC=90°+
∠BAC=90°+20°=110°．故填110°．分析：（1）若点O为△ABC的外心，则∠BOC和∠BAC是同弧所对的圆心角和圆周角，利用圆周角定理可求出∠BOC．
（2）若点O为△ABC的内心，利用结论∠BOC=90°+
∠BAC可计算出∠BOC．点评：理解三角形外心和内心的定义，熟悉圆周角定理，记住三角形两内角的平分线的夹角等于90度与第三个角一半的和，是解决本题的关键．
练习册系列答案
相关题目
25、如图，点E在△ABC外部，点D在边BC上，DE交AC于F．若∠1=∠2=∠3，AC=AE，请说明△ABC≌△ADE的道理．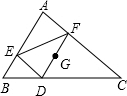
AC于点F．又知BC=5．
10、已知：如图，点D在△ABC的边BC上，DE∥AC交AB于E，DF∥AB交AC于F．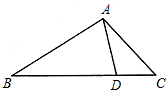
如图，点D在△ABC边BC上，且∠ADC=∠BAC，若AC=x，CD=x-2，BD=2x-2，则x的值是
如图，点D在△ABC的边BC上，DC=AC=BD，∠ACB的平分线CF交AD于F，点E是AB的中点，连接EF．