Question

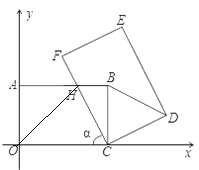
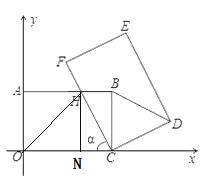
【题目】如图，在平面直角坐标系xOy中，把矩形COAB绕点C顺时针旋转α角，得到矩形CFED．设FC与AB交于点H，且A（0，3），C（5，0）．

（1）当α=60°时，△CBD的形状是　_________　；

（2）当0°＜α＜90°旋转过程中，连结OH,当△OHC为等腰三角形时，请直接写出点H的坐标.

Answer 1

【答案】等边三角形

【解析】分析：（1）根据旋转的性质可得BC=CD，∠BCD=∠α=60°，根据有一个角为60°的等腰三角形为等边三角形，即可得△BCD是等边三角形；（2）分OH=OC，OH=HC，OC=CH三种情况求点H的坐标.

详解：

（1）∵图形旋转后BC=CD，∠BCD=∠α=60°，

∴△BCD是等边三角形；

（2）当OH=OC时，

∵C（5，0），

∴OC=OH=5.

在Rt△AOH中，根据勾股定理求得AH=4，

∴H（4，3）；

当OH=HC时，

过点H作HN垂直于OC于点N，根据等腰三角形的三线合一的性质可得OM=MC=2.5,

∴H（2.5，3）；

当OC=HC时，

过点H作HM垂直于OC于点M，

在Rt△AOH中，根据勾股定理求得CN=4，

∴ON=OC-CN=5-4=1，

∴H（1，3）；

综上，H点的坐标是（1，3），（2.5，3），（4，3）.