题目内容
 (2013•昌平区二模)(1)【原题呈现】如图,要在燃气管道l上修建一个泵站分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
(2013•昌平区二模)(1)【原题呈现】如图,要在燃气管道l上修建一个泵站分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?解决问题:请你在所给图中画出泵站P的位置,并保留作图痕迹;
(2)【问题拓展】已知a>0,b>0,且a+b=2,写出m=
| a2+1 |
| b2+4 |
(3)【问题延伸】已知a>0,b>0,写出以
| a2+b2 |
| a2+4b2 |
| 4a2+b2 |
分析:(1)作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短;
(2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,那么m表示线段MN上任意一点到A的距离与这一点到B的距离之和,根据两点之间线段最短可知,这一点在直线AB上时,距离最小.根据勾股定理即可求出m的最小值;
(3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,则
、
、
是这个三角形的三条边,根据S△CEF=S长方形ABCD-S△AEF-S△CDF-S△CEB即可求解.
(2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,那么m表示线段MN上任意一点到A的距离与这一点到B的距离之和,根据两点之间线段最短可知,这一点在直线AB上时,距离最小.根据勾股定理即可求出m的最小值;
(3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,则
| a2+b2 |
| a2+4b2 |
| 4a2+b2 |
解答: 解:(1)作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短.理由如下:
解:(1)作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短.理由如下:
在直线l上任取一点E,连接AE、BE、A′E,
∵A、A′关于直线l对称,
∴AP=A′P,
同理AE=A′E,
∵AP+BP=A′P+BP=A′B,
AE+BE=A′E+BE>A′B,
∴AP+BP<A′E+BE,
∵E是任意取的一点,
∴AP+BP最短;
 (2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,
(2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,
那么m表示线段MN上任意一点到A的距离与这一点到B的距离之和,
根据两点之间线段最短可知,这一点在直线AB上时,距离最小.
连接AB,交MN于P,则此时m的最小值为线段AB的长.
过B作AM的垂线,交AM的延长线于点C.
在Rt△ABC中,∵AC=1+2=3,BC=2,
∴AB=
=
.
故m的最小值为
;
 (3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,
(3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,
则
、
、
是这个三角形的三条边,
S△CEF=S长方形ABCD-S△AEF-S△CDF-S△CEB
=2a•2b-
•a•b-
•a•2b-
•2a•b
=4ab-
ab-ab-ab
=
ab.
 解:(1)作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短.理由如下:
解:(1)作A关于直线l的对称点A′,连接A′B交直线l于P,连接AP,则泵站修在管道的P点处,可使所用的输气管线AP+BP最短.理由如下:在直线l上任取一点E,连接AE、BE、A′E,
∵A、A′关于直线l对称,
∴AP=A′P,
同理AE=A′E,
∵AP+BP=A′P+BP=A′B,
AE+BE=A′E+BE>A′B,
∴AP+BP<A′E+BE,
∵E是任意取的一点,
∴AP+BP最短;
 (2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,
(2)作线段MN=2,过M作MN的垂线段MA,使MA=1,过N作MN的垂线段NB,使NB=2,且A,B在MN异侧,那么m表示线段MN上任意一点到A的距离与这一点到B的距离之和,
根据两点之间线段最短可知,这一点在直线AB上时,距离最小.
连接AB,交MN于P,则此时m的最小值为线段AB的长.
过B作AM的垂线,交AM的延长线于点C.
在Rt△ABC中,∵AC=1+2=3,BC=2,
∴AB=
| AC2+BC2 |
| 13 |
故m的最小值为
| 13 |
 (3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,
(3)作一个长方形ABCD,设AB=2b,AD=2a,取AB中点E,AD中点F,连接EF,FC,CE,得△EFC,则
| a2+b2 |
| a2+4b2 |
| 4a2+b2 |
S△CEF=S长方形ABCD-S△AEF-S△CDF-S△CEB
=2a•2b-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4ab-
| 1 |
| 2 |
=
| 3 |
| 2 |
点评:本题主要考查轴对称-最短路线问题在实际中的应用,能画出符合要求的图形是解题的关键.

练习册系列答案
相关题目
 (2013•昌平区二模)如图,AC∥FE,点F、C在BD上,AC=DF,BC=EF.
(2013•昌平区二模)如图,AC∥FE,点F、C在BD上,AC=DF,BC=EF. (2013•昌平区二模)在水平的讲台桌上放置圆柱形笔筒和长方体形粉笔盒(如图),则它的主视图是( )
(2013•昌平区二模)在水平的讲台桌上放置圆柱形笔筒和长方体形粉笔盒(如图),则它的主视图是( )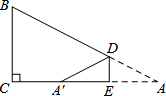 (2013•昌平区二模)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
(2013•昌平区二模)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( ) (2013•昌平区二模)正三角形ABC的边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC2,则y关于x的函数的图象大致为( )
(2013•昌平区二模)正三角形ABC的边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC2,则y关于x的函数的图象大致为( )