题目内容
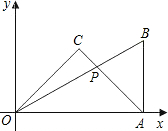 慧慧在一次数学课上,将一副30°,60°,90°和45°,45°,90°的三角板如图放到坐标系中,发现点A的坐标刚好为(9+3
慧慧在一次数学课上,将一副30°,60°,90°和45°,45°,90°的三角板如图放到坐标系中,发现点A的坐标刚好为(9+3| 3 |
分析:过点P作PD⊥x轴,垂足为点D.
OA=9+3
,因为∠AOB=30°,得AB=3+3
;又∠PAD=45°,则PD=AD.
△POD与△BOA相似,则
=
,求得PD、OD,从而得P点坐标.
OA=9+3
| 3 |
| 3 |
△POD与△BOA相似,则
| PD |
| OA-PD |
| AB |
| OA |
解答: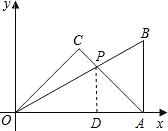 解:过点P作PD⊥x轴,垂足为点D.
解:过点P作PD⊥x轴,垂足为点D.
∵OA=9+3
,∠AOB=30°,
∴tan30°=
,
∴AB=3+3
.
在直角△POD中,∠PAD=45°,
∴PD=AD.
∴△POD∽△BOA.
∴
=
,即
=
,
解得PD=3
,OD=9+3
-3
=9.
∴点P坐标是(9,3
).
 解:过点P作PD⊥x轴,垂足为点D.
解:过点P作PD⊥x轴,垂足为点D.∵OA=9+3
| 3 |
∴tan30°=
| AB | ||
9+3
|
∴AB=3+3
| 3 |
在直角△POD中,∠PAD=45°,
∴PD=AD.
∴△POD∽△BOA.
∴
| PD |
| OA-PD |
| AB |
| OA |
| PD | ||
9+3
|
3+3
| ||
9+3
|
解得PD=3
| 3 |
| 3 |
| 3 |
∴点P坐标是(9,3
| 3 |
点评:本题主要是对解直角三角形,相似三角形的性质及坐标与图形性质等知识的考查,综合性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
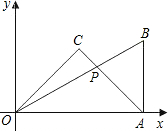 慧慧在一次数学课上,将一副30°,60°,90°和45°,45°,90°的三角板如图放到坐标系中,发现点A的坐标刚好为(9+3
慧慧在一次数学课上,将一副30°,60°,90°和45°,45°,90°的三角板如图放到坐标系中,发现点A的坐标刚好为(9+3 ,0),则图中两块三角板的交点P的坐标是________.
,0),则图中两块三角板的交点P的坐标是________. ,0),则图中两块三角板的交点P的坐标是 .
,0),则图中两块三角板的交点P的坐标是 .