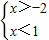题目内容
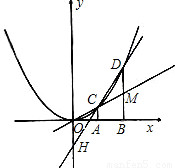
(2010•自贡)如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2图象于点C和D,直线OC交BD于M,直线CD交y轴于点H.记C、D的横坐标分别为xc,xD,于点H的纵坐标yH.(1)证明:①S△CMD:S梯形ABMC=2:3;②xc•xD=-yH;
(2)若将上述A点坐标(1,0)改为A点坐标(t,0)(t>0),其他条件不变,结论S△CMD:S梯形ABMC=2:3是否仍成立?请说明理由.
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么xc,xD和yH又有怎样的数量关系?写出关系式,并证明.

【答案】分析:(1)由题意易求得A、B的坐标,将它们的横坐标代入抛物线的解析式中即可求出C、D的坐标;
①首先求出直线OC的解析式,联立B点的横坐标即可求出M点的坐标;以DM为底,A、B横坐标差的绝对值为高,可求出△CMD的面积;同理可根据梯形的面积公式求出梯形ABMC的面积,进而可判断出所求的结论是否正确;
②用待定系数法易求得直线CD的解析式,即可得到H点的坐标,然后再判断所求的结论是否正确.
(2)的解法同(1);
(3)由于二次函数的解析式为y=ax2(a>0),且点A的坐标为(t,0)时,点C的坐标为(t,at2),点D的坐标为(2t,4at2),然后设直线CD的解析式为y=kx+b,利用待定系数法即可求出CD的函数解析式,接着得到H的坐标为(0,-2at2),也就得到题目的结论.
解答:(1)证明:由已知可得点B的坐标为(2,0),点C的坐标为(1,1),点D的坐标为(2,4),且
直线OC的函数解析式为y=x.
∴点M的坐标为(2,2),易得S△CMD=1,S梯形ABMC= (1.5分)
(1.5分)
∴S△CMD:S梯形ABMC=2:3,即结论①成立.
设直线CD的函数解析式为y=kx+b,
则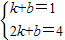 ,
,
即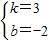 ;
;
∴直线CD的解析式为y=3x-2.
由上述可得点H的坐标为(0,-2),
即yH=-2(2.5分)
∴xC•xD=-yH.
即结论②成立(3分)
(2)解:结论S△CMD:S梯形ABMC=2:3仍成立;(4分)
理由如下:∵点A的坐标为(t,0),(t>0);
则点B的坐标为(2t,0)
从而点C的坐标为(t,t2),点D的坐标为(2t,4t2);
设直线OC的解析式为y=kx,则t2=kt得k=t
∴直线OC的解析式为y=tx(5分)
又设M的坐标为(2t,y)
∵点M在直线OC上
∴当x=2t时,y=2t2
∴点M的坐标为(2t,2t2)(6分)
∴S△CMD:S梯形ABMC= •2t2•t:
•2t2•t: (t2+2t2)•t
(t2+2t2)•t
=t3:( t3)
t3)
= (7分)
(7分)
(3)解:xC,xD和yH有关数量关系xC•xD=- yH(8分)
yH(8分)
由题意,当二次函数的解析式为y=ax2(a>0),且点A的坐标为(t,0)时,点C的坐标为(t,at2),点D的坐标为(2t,4at2)(9分)
设直线CD的解析式为y=kx+b
则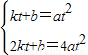 ,
,
得 ;
;
∴CD的解析式为y=3atx-2at2(11分)
则H的坐标为(0,-2at2)
即yH=-2at2(11.5分)
∵xC•xD=t•2t=2t2(12分)
∴xC•xD=- yH.
yH.
点评:此题主要考查了函数图象交点坐标及图形面积的求法,综合性强,能力要求较高.
①首先求出直线OC的解析式,联立B点的横坐标即可求出M点的坐标;以DM为底,A、B横坐标差的绝对值为高,可求出△CMD的面积;同理可根据梯形的面积公式求出梯形ABMC的面积,进而可判断出所求的结论是否正确;
②用待定系数法易求得直线CD的解析式,即可得到H点的坐标,然后再判断所求的结论是否正确.
(2)的解法同(1);
(3)由于二次函数的解析式为y=ax2(a>0),且点A的坐标为(t,0)时,点C的坐标为(t,at2),点D的坐标为(2t,4at2),然后设直线CD的解析式为y=kx+b,利用待定系数法即可求出CD的函数解析式,接着得到H的坐标为(0,-2at2),也就得到题目的结论.
解答:(1)证明:由已知可得点B的坐标为(2,0),点C的坐标为(1,1),点D的坐标为(2,4),且
直线OC的函数解析式为y=x.
∴点M的坐标为(2,2),易得S△CMD=1,S梯形ABMC=
 (1.5分)
(1.5分)∴S△CMD:S梯形ABMC=2:3,即结论①成立.
设直线CD的函数解析式为y=kx+b,
则
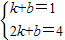 ,
,即
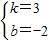 ;
;∴直线CD的解析式为y=3x-2.
由上述可得点H的坐标为(0,-2),
即yH=-2(2.5分)
∴xC•xD=-yH.
即结论②成立(3分)
(2)解:结论S△CMD:S梯形ABMC=2:3仍成立;(4分)
理由如下:∵点A的坐标为(t,0),(t>0);
则点B的坐标为(2t,0)
从而点C的坐标为(t,t2),点D的坐标为(2t,4t2);
设直线OC的解析式为y=kx,则t2=kt得k=t
∴直线OC的解析式为y=tx(5分)
又设M的坐标为(2t,y)
∵点M在直线OC上
∴当x=2t时,y=2t2
∴点M的坐标为(2t,2t2)(6分)
∴S△CMD:S梯形ABMC=
 •2t2•t:
•2t2•t: (t2+2t2)•t
(t2+2t2)•t=t3:(
 t3)
t3)=
 (7分)
(7分)(3)解:xC,xD和yH有关数量关系xC•xD=-
 yH(8分)
yH(8分)由题意,当二次函数的解析式为y=ax2(a>0),且点A的坐标为(t,0)时,点C的坐标为(t,at2),点D的坐标为(2t,4at2)(9分)
设直线CD的解析式为y=kx+b
则
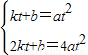 ,
,得
 ;
;∴CD的解析式为y=3atx-2at2(11分)
则H的坐标为(0,-2at2)
即yH=-2at2(11.5分)
∵xC•xD=t•2t=2t2(12分)
∴xC•xD=-
 yH.
yH.点评:此题主要考查了函数图象交点坐标及图形面积的求法,综合性强,能力要求较高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目