Question

设有关于x的一元二次方程x²+2ax+b²=0．
（Ⅰ）若a是从0，1，2三个数中任取一个数，b是从0，1两个数中任取的一个数，求上述方程有实根的概率．
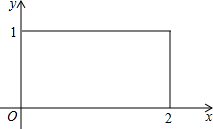
（Ⅱ）若在如图所示的矩形内任取一点P，设P的横坐标为a，纵坐标为b，求上述方程有实根的概率．

Answer 1

（1）△=4a²-4b²=4（a²-b²），
画树状图，
共有6种等可能的结果，其中只有a=0，b=1使△＜0，即使△≥0有5种情况，
所以方程有实根的概率=

5

6

；
（2）如图，OD平分∠AOC，
当点P落在四边形OABD内时，a≥b，则原方程有实数根，
而S_△OCD=

1

2

×1×1=

1

2

，S_矩形OABC=2，
所以方程有实根的概率=

2- 1 2

2

=

3

4

．