题目内容
【题目】在等边△ABC中,
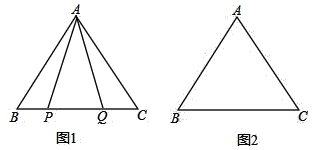
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;②小明通过观察、实验,提出猜想:在点P,Q运动的过程中,始终有PA=PM,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证PA=PM,只需证△APM是等边三角形.
想法2:在BA上取一点N,使得BN=BP,要证PA=PM,只需证△ANP≌△PCM.……
请你参考上面的想法,帮助小明证明PA=PM(一种方法即可).
【答案】(1)80°;(2)见解析
【解析】
对于(1)根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,根据三角形外角的性质即可得到结论;
对于(2)①根据题意和轴对称的性质即可画出图形;
②如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.
(1)∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ=20°,
∴∠AQB=∠APQ=∠BAP+∠B=80°;
(2)①补全的图如图所示.
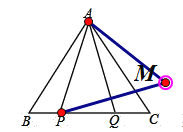
![]()
②∵AP=AQ,
∴∠APQ=∠AQP,
∴∠APB=∠AQC,
∴△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠BAP=∠CAQ.
∵点Q关于直线AC的对称点为M,
∴AQ=AM,∠QAC=∠MAC,
∴∠MAC=∠BAP,
∴∠BAP+∠PAC=∠MAC+∠CAP=60°,
∴∠PAM=60°.
∵AP=AQ,
∴AP=AM,
∴△APM是等边三角形,
∴PA=PM.







