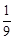题目内容
一项“过关游戏”规定:若闯第n关需将一颗质地均匀的骰子抛掷n次,如果闯第n关时所抛出的所有点数之和大于
n2,则算闯关成功;否则闯关失败.下列说法中正确的是( )
| 3 |
| 4 |
分析:根据概率公式,找准两点:符合条件的情况数目;全部情况的总数.二者的比值就是其发生的概率的大小.
解答:解:A、第1关,抛掷1次出现的点数最小为1,而抛出的所有点数之和大于
n2就行,故一定过关,故此选项错误;
B、因为过第三关要求这3次抛掷所出现的点数之和大于
×32=
,
由题设可知事件A是指第三关出现点数之和没有大于7.
因为第三关出现点数之和为3,4,5,6,7的次数分别为1,3,6,6,9,
∴P(小于7的概率)=
,
∴P( 大于7的概率)=1-
=
.故此选项错误;
C、过第二关要求这2次抛掷所出现的点数之和大于
×22=3,所以过第二关的概率是1-
=
;故此选项正确;
D、过第六关要求这6次抛掷所出现的点数之和大于
×62=27,而抛6次出现的点数之和最大为36,所以出现27是有可能的,故此选项错误.
故选:C.
| 3 |
| 4 |
B、因为过第三关要求这3次抛掷所出现的点数之和大于
| 3 |
| 4 |
| 27 |
| 4 |
由题设可知事件A是指第三关出现点数之和没有大于7.
因为第三关出现点数之和为3,4,5,6,7的次数分别为1,3,6,6,9,
∴P(小于7的概率)=
| 25 |
| 108 |
∴P( 大于7的概率)=1-
| 25 |
| 108 |
| 83 |
| 108 |
C、过第二关要求这2次抛掷所出现的点数之和大于
| 3 |
| 4 |
| 3 |
| 36 |
| 11 |
| 12 |
D、过第六关要求这6次抛掷所出现的点数之和大于
| 3 |
| 4 |
故选:C.
点评:此题考查了概率公式的使用和可能性大小的判断,相互独立事件同时发生的概率,考查离散型随机变量的分布列和期望,本题的数字运算比较麻烦,注意不要出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
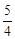 n2,则算过关;否则不算过关,则能过第二关的概率是
n2,则算过关;否则不算过关,则能过第二关的概率是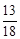 B.
B.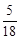 C.
C.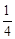 D.
D.