题目内容
【题目】如图,设一个三角形的三边分别是3,13m,8.

(1)求m的取值范围;
(2)是否存在整数m使三角形的周长为偶数?若存在,求出三角形的周长;若不存在,说明理由;
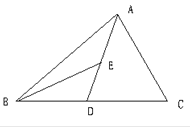
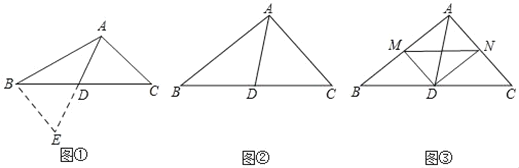
(3)如图,在(2)的条件下,当AB=8,AC=13m,BC=3时,若D是AB的中点,连CD,P是CD上动点(不与C,D重合,当P在线段CD上运动时,有两个式子):①![]() ;②
;②![]() ,其中有一个的值不变,另一个的值改变。问题:
,其中有一个的值不变,另一个的值改变。问题:
A.请判断出谁不变,谁改变;
B.若不变的求出其值,若改变的求出变化的范围。
【答案】(1)![]() ;(2) 存在,理由见解析;(3) ①不改变,②改变,
;(2) 存在,理由见解析;(3) ①不改变,②改变,![]()
【解析】
(1) 根据三角形的三边关系即可求得;
(2)由(1)求得的 m取值范围,取整数,通过计算可得;
(3)利用等底等高的两个三角形面积相等以及三角形两边之和大于第三边的性质,通过计算可以求得答案.
(1)由三角形三边关系可得![]() ,解得
,解得![]() ;
;
(2)存在,理由是:
∵![]() ;
;
∴![]() 为整数的时候取值可为-3或-2,
为整数的时候取值可为-3或-2,
当![]() 时,
时,![]()
∴周长是3+8+10=21,不是偶数;
当![]() 时,
时,![]()
∴周长是![]() ,是偶数,所以存在.
,是偶数,所以存在.
(3)∵点D是AB的中点,则CD是中线,设点A到CD的距离为h,则点B到CD的距离也为h,
∴![]() ,
,![]()
![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() ,
,
∴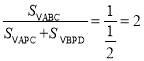
∴①不改变;
∵![]()
∴由三角形两边之和大于第三边性质可以知道![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() .
.
∴②改变.

练习册系列答案
相关题目