题目内容
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线. 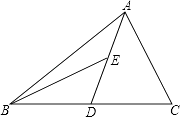
(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为40,BD=5,求EF的长.
【答案】
(1)解;如图所示:
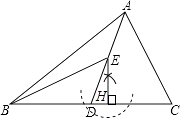
(2)解;∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△ABD= ![]() S△ABC,S△BDE=
S△ABC,S△BDE= ![]() S△ABD,
S△ABD,
∴S△BDE= ![]() S△ABC,
S△ABC,
∵△ABC的面积为40,BD=5,
∴ ![]() ×5×EF=10,
×5×EF=10,
∴EF=4
【解析】(1)根据过直线外一点作已知直线的垂线的方法作图即可;(2)利用三角形中线的性质得出S△BDE= ![]() S△ABC , 进而借助三角形面积公式求出即可.
S△ABC , 进而借助三角形面积公式求出即可.
【考点精析】掌握三角形的面积是解答本题的根本,需要知道三角形的面积=1/2×底×高.

练习册系列答案
相关题目
【题目】根据下列表格回答问题:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)268.96的算术平方根是__________;
(2)![]() =___________;
=___________;
(3)![]() 在哪两个相邻的一位小数之间?为什么?
在哪两个相邻的一位小数之间?为什么?