题目内容
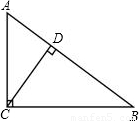
如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC= .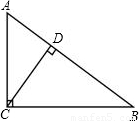
【答案】分析:由三角形的性质:直角三角形中,斜边上的高是两条直角边在斜边上的射影比例中项,即CD2=AD×BD,可将BD的长求出,然后在Rt△BCD中,根据勾股定理可将BC的边求出.
解答:解:∵若CD是Rt△ABC斜边上的高,AD=3,CD=4
∴CD2=AD×BD,即42=3×BD解得:BD=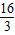
在Rt△BCD中,∵BC2=CD2+BD2,
∴BC= =
=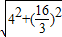 =
=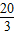 .
.
点评:本题主要考查三角形的性质及对勾股定理的应用.
解答:解:∵若CD是Rt△ABC斜边上的高,AD=3,CD=4
∴CD2=AD×BD,即42=3×BD解得:BD=
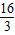
在Rt△BCD中,∵BC2=CD2+BD2,
∴BC=
 =
=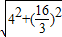 =
=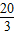 .
.点评:本题主要考查三角形的性质及对勾股定理的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
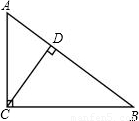
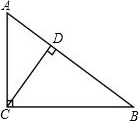 如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=
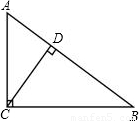
如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=