题目内容
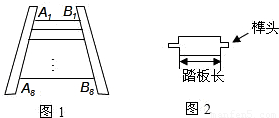
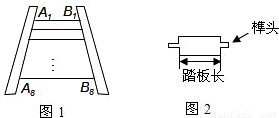
王大伯要做一张如图1的梯子，梯子共有8级互相平行的踏板，每相邻两级踏板之间的距离都相等．已知梯子最上面一级踏板的长度A1B1=0.5m，最下面一级踏板的长度A8B8=0.8m．木工师傅在制作这些踏板时，截取的木板要比踏板长，以保证在每级踏板的两个外端各做出一个长为4cm的榫头（如图2所示），以此来固定踏板．现市场上有长度为2.1m的木板可以用来制作梯子的踏板（木板的宽厚和厚度正好符合要制作梯子踏板的要求），请问：制作这些踏板，王大伯最少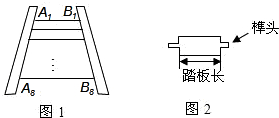
需要买几块这样的木板？请说明理由．（不考虑锯缝的损耗）
分析：在解此题的过程中，一定要构建相似三角形，因为踏板之间是相互平行，而且间隔相等，所以可利用这一组平行线来构建相似三角形，从而依次求出自上而下各条踏板的长度．另外千万不要忽略榫头的长度；
解法二：可以把梯子看做一个等腰梯形，由中位线定理即可求解；
解法三：和解法二相同，都是利用梯形中位线，只不过又做了一条踏板A9B9，有A1B1和A9B9能求出A5B5，然后有A5B5和A9B9求出A7B7，再有A7B7和A9B9求出A8B8=80，从而算出A9B9的具体数值，这样的话，A1B1至A8B8的长就都能准确求出，从而算出一共需要多少材料．
解法二：可以把梯子看做一个等腰梯形，由中位线定理即可求解；
解法三：和解法二相同，都是利用梯形中位线，只不过又做了一条踏板A9B9，有A1B1和A9B9能求出A5B5，然后有A5B5和A9B9求出A7B7，再有A7B7和A9B9求出A8B8=80，从而算出A9B9的具体数值，这样的话，A1B1至A8B8的长就都能准确求出，从而算出一共需要多少材料．
解答：解：法一：如图，设自上往下第2，3，4，5，6，7级踏板的长依次为A2B2，A3B3，A7B7，过A1作B1B8的平行线分别交A2B2，A3B3，A8B8于点C2，C3，…，C8．
∵每两级踏板之间的距离相等，
∴C8B8=C7B7=…=C2B2=A1B1=50cm，A8C8=80-50=30cm．
∵A2C2∥A8B8，
∴∠A1A2C2=∠A1A8C8，∠A1C2A2=∠A1C8A8，
∴△A1A2C2∽△A1A8C8，
∴A2C2：A8C8=1：7，
∴A2C2=
，
∴A2B2=50+
，
设要制作A1B1，A2B2，…，A7B7，A8B8这些踏板需用木板的长度分别为a1cm，a2cm，…，a8cm，
则a1=50+8=58，a2=50+
+8=58+
，a3=58+
，a4=58+
，a5=58+
，a6=58+
，a7=58+
，a8=58+30，
∵a1+a2+a3+a4=232+
＞210，
∴王大伯买的木板肯定不能少于3块，
又∵a1+a3+a6=174+
=204＜210，
a2+a4+a5=174+
＜174+
=210，
a7+a8=146+
=171
＜210，
∴王大伯最少买3块这样的木板就行了．
法二：如图，分别取A1A8，B1B8的中点P，Q，连接PQ．
设自上往下第2，3，4，5，6，7级踏板的长依次为A2B2，A3B3，…，A7B7，则由梯形中位线定理可得：
A1B1+A8B8=A2B2+A7B7=A3B3+A6B6=A4B4+A5B5=2PQ．（2分）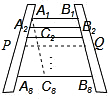
∵A1B1=50cm，A8B8=80cm，
∴A1B1+A8B8=A2B2+A7B7=A3B3+A6B6=A4B4+A5B5=130．（3分）
设要制作A1B1，A2B2，…，A7B7，A8B8，
这些踏板需用木板的长度为a1cm，a2cm，…，a8cm，
则a1+a8=a2+a7=a3+a6=a4+a5=146．
∵a1+a2+…+a8=146×4=584＞210×2，
∴王大伯买的木板肯定不能少于3块．（4分）
过A1作B1B8的平行线分别交A2B2，A3B3，…，A8B8，
于点C2，C3，…，C8．
∵每两级踏板之间的距离相等，
∴C8B8=C7B7=…=C2B2=A1B1=50cm，A8C8=80-50=30cm．
∵A2C2∥A8B8，
∴∠A1A2C2=∠A1A8C8，∠A1C2A2=∠A1C8A8，
∴△A1A2C2∽△A1A8C8，
∴A2C2：A8C8=1：7，
∴A2C2=
，
∴A2B2=50+
，（6分）
∴a2=58+
．
而a1=58，a8=88，
∴a1+a3+a6=58+146=204＜210，a2+a4+a5=58+
+146=204+
＜210，a7+a8＜a8+a8=88×2＜210．
∴王大伯最少买3块这样的木板就行了．（8分）
法三：如果在梯子的下面再做第9级踏板，
它与其上面一级踏板之间的距离等于梯子相邻两级踏板之间的距离（如图），
设第9级踏板的长为xcm，
则由梯形中位线的性质可得：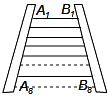
第5级踏板的长A5B5=
（50+x）cm，
第7级踏板的长A7B7=
[
（50+x）+x]cm，
由题意得：
第8级踏板的长A8B8=
{
[
（50+x）+x]+x}=80，
解这个方程得：
x=84
，（2分）
由此可求得：
A7B7=75
cm，A5B5=67
cm，A6B6=71
cm，A3B3=58
cm，A2B2=54
cm，A4B4=62
cm．
设要制作A1B1，A2B2，…，A7B7，A8B8，这些踏板需截取的木板长度分别为a1cm，a2cm，…，a8cm，
则a1=50+8=58，a2=62
，a3=66
，a4=70
，a5=75
，a6=79
，a7=83
，a8=88．
∴a1+a3+a6=58+146=204＜210，a2+a4+a5=58+
+146=204+
＜210，a7+a8＜a8+a8=88×2＜210．
∴王大伯最少买3块这样的木板就行了（5分）
∵每两级踏板之间的距离相等，
∴C8B8=C7B7=…=C2B2=A1B1=50cm，A8C8=80-50=30cm．
∵A2C2∥A8B8，
∴∠A1A2C2=∠A1A8C8，∠A1C2A2=∠A1C8A8，
∴△A1A2C2∽△A1A8C8，
∴A2C2：A8C8=1：7，
∴A2C2=
| 30 |
| 7 |
∴A2B2=50+
| 30 |
| 7 |
设要制作A1B1，A2B2，…，A7B7，A8B8这些踏板需用木板的长度分别为a1cm，a2cm，…，a8cm，
则a1=50+8=58，a2=50+
| 30 |
| 7 |
| 30 |
| 7 |
| 60 |
| 7 |
| 90 |
| 7 |
| 120 |
| 7 |
| 150 |
| 7 |
| 180 |
| 7 |
∵a1+a2+a3+a4=232+
| 180 |
| 7 |
∴王大伯买的木板肯定不能少于3块，
又∵a1+a3+a6=174+
| 210 |
| 7 |
a2+a4+a5=174+
| 240 |
| 7 |
| 252 |
| 7 |
a7+a8=146+
| 180 |
| 7 |
| 5 |
| 7 |
∴王大伯最少买3块这样的木板就行了．
法二：如图，分别取A1A8，B1B8的中点P，Q，连接PQ．
设自上往下第2，3，4，5，6，7级踏板的长依次为A2B2，A3B3，…，A7B7，则由梯形中位线定理可得：
A1B1+A8B8=A2B2+A7B7=A3B3+A6B6=A4B4+A5B5=2PQ．（2分）
∵A1B1=50cm，A8B8=80cm，
∴A1B1+A8B8=A2B2+A7B7=A3B3+A6B6=A4B4+A5B5=130．（3分）
设要制作A1B1，A2B2，…，A7B7，A8B8，
这些踏板需用木板的长度为a1cm，a2cm，…，a8cm，
则a1+a8=a2+a7=a3+a6=a4+a5=146．
∵a1+a2+…+a8=146×4=584＞210×2，
∴王大伯买的木板肯定不能少于3块．（4分）
过A1作B1B8的平行线分别交A2B2，A3B3，…，A8B8，
于点C2，C3，…，C8．
∵每两级踏板之间的距离相等，
∴C8B8=C7B7=…=C2B2=A1B1=50cm，A8C8=80-50=30cm．
∵A2C2∥A8B8，
∴∠A1A2C2=∠A1A8C8，∠A1C2A2=∠A1C8A8，
∴△A1A2C2∽△A1A8C8，
∴A2C2：A8C8=1：7，
∴A2C2=
| 30 |
| 7 |
∴A2B2=50+
| 30 |
| 7 |
∴a2=58+
| 30 |
| 7 |
而a1=58，a8=88，
∴a1+a3+a6=58+146=204＜210，a2+a4+a5=58+
| 30 |
| 7 |
| 30 |
| 7 |
∴王大伯最少买3块这样的木板就行了．（8分）
法三：如果在梯子的下面再做第9级踏板，
它与其上面一级踏板之间的距离等于梯子相邻两级踏板之间的距离（如图），
设第9级踏板的长为xcm，
则由梯形中位线的性质可得：
第5级踏板的长A5B5=
| 1 |
| 2 |
第7级踏板的长A7B7=
| 1 |
| 2 |
| 1 |
| 2 |
由题意得：
第8级踏板的长A8B8=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解这个方程得：
x=84
| 2 |
| 7 |
由此可求得：
A7B7=75
| 5 |
| 7 |
| 1 |
| 7 |
| 3 |
| 7 |
| 4 |
| 7 |
| 2 |
| 7 |
| 6 |
| 7 |
设要制作A1B1，A2B2，…，A7B7，A8B8，这些踏板需截取的木板长度分别为a1cm，a2cm，…，a8cm，
则a1=50+8=58，a2=62
| 2 |
| 7 |
| 2 |
| 7 |
| 6 |
| 7 |
| 1 |
| 7 |
| 3 |
| 7 |
| 5 |
| 7 |
∴a1+a3+a6=58+146=204＜210，a2+a4+a5=58+
| 30 |
| 7 |
| 30 |
| 7 |
∴王大伯最少买3块这样的木板就行了（5分）
点评：此题构建相似三角形是关键，只要将实际问题转化为数学问题，利用相似比即可求出，相对来讲，方法三还是比较简单的．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
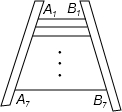王大伯要做一张如图所示的梯子，梯子共有7级互相平行的踏板，每相邻两级踏板之间的距离都相等．已知梯子最上面一级踏板的长度A1B1=0.5m，最下面一级踏板的长度A7B7=0.8m．则A3B3踏板的长度为（ ）| A、0.6m | B、0.65m | C、0.7m | D、0.75m |
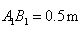，最下面一级踏板的长度
．木工师傅在制作这些踏板时，截取的木板要比踏板长，以保证在每级踏板的两个外端各做出一个长为4cm的榫头（如图2所示），以此来固定踏板．现市场上有长度为2.1m的木板可以用来制作梯子的踏板（木板的宽厚和厚度正好符合要制作梯子踏板的要求），请问：制作这些踏板，王大伯最少需要买几块这样的木板？请说明理由．（不考虑锯缝的损耗）
