题目内容
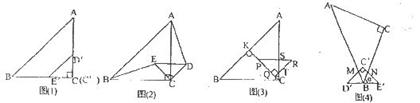
如图(1)是腰长分别是![]() 和2的两个等腰直角三角形ABC和C‘D‘E‘叠放在一起(C与C’重合).
和2的两个等腰直角三角形ABC和C‘D‘E‘叠放在一起(C与C’重合).
(1)固定△ABC,将△C‘D‘E‘绕点C顺时针旋转45°得到△CDE,如图(2),若连结BE、 AD,请你判断BE与AD的大小关系,并证明你的结论;
(2)延长CE交AB于K点,将图(2)中的△CDE在线段CK上沿着CK方向以每秒1个单位长度的速度平移,如图(3),将平移后的△CDE设为△PQR,设△PQR移动的时间为x秒,点P运动到K点停止,设△PQR与△AKC重叠的面积为y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)将△D‘E‘C‘按如图(4)固定,将△ABC一锐角顶点B落在斜边E’D’的中点,然后绕B点逆时针旋转![]() 度,使边AB交D’C’于点M,边BC交E’C’于点N.
度,使边AB交D’C’于点M,边BC交E’C’于点N.
请你探究:图(4)的D’M?E’N的值是否随![]() 的变化而变化?如果没有变化,请求出D’M?E’N的值,并说明理由;如果有变化,也请说明理由.
的变化而变化?如果没有变化,请求出D’M?E’N的值,并说明理由;如果有变化,也请说明理由.
解:(1)BE=AD
∵BC=AC,CE=CD,∠BCE=∠ACD
∴△BCE∽△ACD (SAS) ∴BE=AD
(2)∵QT=QC=x,RT=2-x,ST=![]() (2-x)
(2-x)
当点P运动到点K时,点R恰好运动到AC的中点(学生不回答这一点,不扣分),
∴![]()
即y=-![]() x2+x+1
x2+x+1
∵AC=![]() ,∴CK=4
,∴CK=4
∴点P运动的距离为4-2=2.
∴自变量x的取值范围是0≤x≤2.
(3)D’M?E’N的值不随![]() 的变化而变化。
的变化而变化。
在△D’BM和△E’NB中,
∵∠D’BM=135°-∠![]() =∠E’NB ∠D’=∠E’
=∠E’NB ∠D’=∠E’
∴△D’BM∽△E’NB
∴D’M?E’N=D’B?E’B=![]() =2
=2

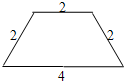 33、如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
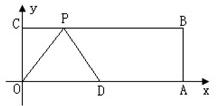
33、如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.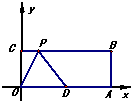 12、已知:如图,在直角坐标系中,O为坐标原点,四边形OABC为矩形,A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为
12、已知:如图,在直角坐标系中,O为坐标原点,四边形OABC为矩形,A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为
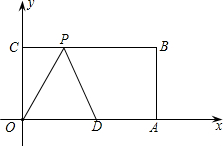 已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),
已知如图,平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点C,点D的坐标分别为(0,4),(5,0),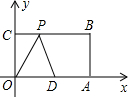 已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为
已知如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(20,0),C(0,8),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为10的等腰三角形时,点P的坐标为