题目内容
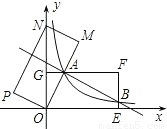
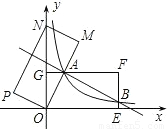
（2009•天水）如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为（4，0），顶点G的坐标为（0，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．（1）判断△OGA和△OMN是否相似，并说明理由；
（2）求图象经过点A的反比例函数的解析式；
（3）设（2）中的反比例函数图象交EF于点B，求直线AB的解析式．
【答案】分析：（1）根据两个角对应相等，即可证明两个三角形相似；
（2）要求反比例函数的解析式，则需求得点A的坐标，即要求得AG的长，根据旋转的两个图形全等的性质以及相似三角形的对应边的比相等可以求解；
（3）要求直线AB的解析式，主要应求得点B的坐标．根据点B的横坐标是4和（2）中求得的反比例函数的解析式即可求得．再根据待定系数法进行求解．
解答：解：（1）△OGA∽△OMN，
理由：
∵∠OGA=∠M=90°，
∠GOA=∠MON
∴△OGA∽△OMN；
（2）由（1）得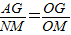
，
∴
，
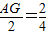∴AG=1，
设反比例函数为y=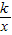
（k不等于0），
把A（1，2）代入得k=2，
∴过点A的反比例函数的解析式为y=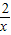
；
（3）∵点B的横坐标为4，
把x=4代入y=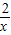
中得y=
，
故B（4，
），
设直线AB的解析式是y=mx+n，
把A（1，2），B（4，
）代入
得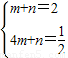
，
解得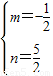
，
∴直线AB的解析式为y=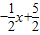
．
点评：此题要求学生：
①能够根据旋转的性质得到对应边相等；
②掌握相似三角形的判定和性质；
③能够运用待定系数法求得函数的解析式，根据函数的解析式确定点的坐标．
（2）要求反比例函数的解析式，则需求得点A的坐标，即要求得AG的长，根据旋转的两个图形全等的性质以及相似三角形的对应边的比相等可以求解；
（3）要求直线AB的解析式，主要应求得点B的坐标．根据点B的横坐标是4和（2）中求得的反比例函数的解析式即可求得．再根据待定系数法进行求解．
解答：解：（1）△OGA∽△OMN，
理由：
∵∠OGA=∠M=90°，
∠GOA=∠MON
∴△OGA∽△OMN；
（2）由（1）得
，∴
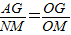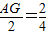，∴AG=1，
设反比例函数为y=
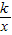（k不等于0），把A（1，2）代入得k=2，
∴过点A的反比例函数的解析式为y=
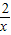；（3）∵点B的横坐标为4，
把x=4代入y=
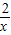中得y=，故B（4，
），设直线AB的解析式是y=mx+n，
把A（1，2），B（4，
）代入得
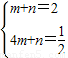，解得
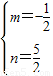，∴直线AB的解析式为y=
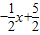．点评：此题要求学生：
①能够根据旋转的性质得到对应边相等；
②掌握相似三角形的判定和性质；
③能够运用待定系数法求得函数的解析式，根据函数的解析式确定点的坐标．
练习册系列答案
相关题目
．
．
．