Question

如图，用长为32米的篱笆围成一个外形为矩形的花圃，花圃的一边利用原有墙，中间用2道篱笆割成3个小矩形.已知原有墙的最大可利用长度为15米，花圃的面积为S平方米，平行于原有墙的一边BC长为x米.

（1）求S关于x的函数关系式；

（2）当围成的花圃面积为60平方米时，求AB的长；

（3）能否围成面积比60平方米更大的花圃？如果能，那么最大的面积是多少？如果不能，请说明理由.

 

Answer 1

【答案】

（1）             

（2）AB的长为5米.    

（3）

 

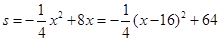
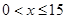∵，S随着x的增大而增大，

 

∴当x=15时，S的最大值是平方米.

【解析】（1）求出S=AB×BC代入即可；

（2）求出方程的解即可；

（3）把解析式化成顶点式，求出顶点的坐标即可得到答案