题目内容
(2003•资阳)若代数式2xm+4y与x2yn-2是同类项,则抛物线y=x2+mx+n的顶点坐标为 .
【答案】分析:根据同类项的定义,列方程组求m、n的值,代入抛物线解析式求顶点坐标.
解答:解:∵代数式2xm+4y与x2yn-2是同类项,
∴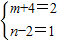 ,解得n=3,m=-2,
,解得n=3,m=-2,
∴抛物线y=x2+mx+n的顶点坐标为
x=-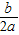 =-
=-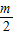 =
= =1;
=1;
y=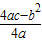 =
=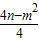 =
=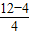 =2;
=2;
故抛物线y=x2+mx+n的顶点坐标为(1,2).
点评:本题综合考查二次函数的顶点坐标公式,同类项的定义.
解答:解:∵代数式2xm+4y与x2yn-2是同类项,
∴
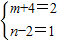 ,解得n=3,m=-2,
,解得n=3,m=-2,∴抛物线y=x2+mx+n的顶点坐标为
x=-
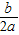 =-
=-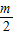 =
= =1;
=1;y=
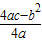 =
=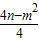 =
=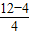 =2;
=2;故抛物线y=x2+mx+n的顶点坐标为(1,2).
点评:本题综合考查二次函数的顶点坐标公式,同类项的定义.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目