题目内容
【题目】![]() .
.![]() 分别是数轴上两个不同点A.B所表示的有理数,且
分别是数轴上两个不同点A.B所表示的有理数,且![]() ,
,![]() ,A.B两点在数轴上的位置如图所示:
,A.B两点在数轴上的位置如图所示:
(1)数![]() =_____;
=_____;![]() =______;
=______;
(2)A.B两点相距多少个单位长度?
(3)点P从A点出发,先向左移动一个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度,依次操作2020次后,求P点表示的数.
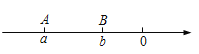
【答案】(1)-5,-2;(2)3;(3)1005
【解析】
(1)根据绝对值求出a,b的值,再结合数轴即可解答;
(2)利用两点间的距离公式进行求解即可;
(3)根据题意列出式子,找出规律进行求解即可.
解:(1)∵|a|=5,|b|=2,
∴a=5或a=-5,b=2或b=-2,
由数轴得:a<b<0,
∴a=-5,b=-2;
(2)由题意可得:
AB=|-2-(-5)|=3.
答:A,B两点相距3个单位长度;
(3)由题意得
-5-1+2-3+4-5+6-…-2019+2020
=-5+(-1+2)+(-3+4)+···+(-2017+2018)+(-2019+2020)
=-5+1010
=1005.

【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师和学生各有多少人?
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
【题目】某农户共摘收水蜜桃1920千克,为寻求合适的销售价格,进行了6天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | |
售价 x(元/千克) | 20 | 18 | 15 | 12 | 10 | 9 |
销售量 y(千克) | 45 | 50 | 60 | 75 | 90 | 100 |
由表中数据可知,试销期间这批水蜜桃的每天销售量y(千克)与售价x(元/千克)之间满足我们曾经学过的某种函数关系.若在这批水蜜桃的后续销售中,每天的销售量y(千克)与售价x(元/千克)之间都满足这一函数关系.
(1)你认为y与x之间满足什么函数关系?并求y关于x的函数表达式.
(2)在试销6天后,该农户决定将这批水密桃的售价定为15元/千克.
① 若每天都按15元/千克的售价销售,则余下的水蜜桃预计还要多少天可以全部售完?
② 该农户按15元/千克的售价销售20天后,发现剩下的水蜜桃过于成熟,必须在不超过2天内全部售完,因此需要重新确定一个售价,使后面2天都按新的售价销售且能如期全部售完,则新的售价最高可以定为多少元/千克?