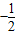题目内容
(2001•昆明)已知:⊙O1与⊙O2外切于点A,直线l与⊙O1、⊙O2相切于B、C两点,且与O1O2的延长线交于点P(如图).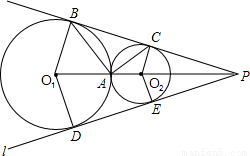
(1)求∠BAC的度数;当l绕P点逆时针移动(过A点时除外),与⊙O1和⊙O2的交点从左到右依次为B、G、F、C时(如图),∠BAC+∠GAF的度数能定吗?若能确定,请求出.
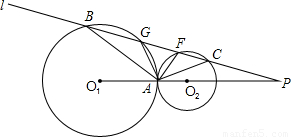
(2)当直线1绕P点移动到两圆的另一侧且与两圆分别相切于D、E时,在图中各找出两组垂直线段和相似三角形.(不再添加辅助线)
【答案】分析:(1)根据如果三角形一边的中线等于这边的一半,那么这个三角形是直角三角形.为此,过点A作两圆的内公切线,交BC于点P.根据切线长定理可得PB=PA=PC,得出∠BAC=90°.∠BAC+∠GAF的度数是否能确定,取决于此二角的度数和是否为一个常数,如果过点A作两圆的内公切线,交BC于点Q,所以GAF=∠B+∠P,从而∠BAC+∠GAF=180°.
(2)根据切线的性质容易知道O1D⊥PD,O2E⊥PE.由O1D∥O2E知:△PO1D∽△PO2E.
解答: 解:(1)过点A作两圆的内公切线,交BC于点Q,
解:(1)过点A作两圆的内公切线,交BC于点Q,
∵⊙O1与⊙O2外切于点A,直线l与⊙O1、⊙O2相切于B、C两点,
∴QB=QA=QC,
∴∠BAC=90°;
当l绕P点逆时针移动(过A点时除外),与⊙O1和⊙O2的交点从左到右依次为B、G、F、C时,∠BAC+∠GAF的度数能确定.过点A作两圆的内公切线,交BC于点Q;
∵⊙O1与⊙O2外切于点A,
∴∠GAQ=∠B,∠FAQ=∠P,
∴∠GAF=∠GAQ+∠FAQ=∠B+∠P;
∵∠BAC+∠B+∠P=180°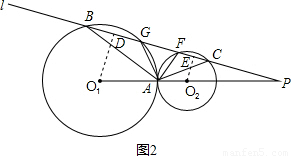 ,
,
∴∠BAC+∠GAF=180°;
(2)垂直线段:O1D⊥PD,O2E⊥PE
相似三角形:△PO1D∽△PO2E.
点评:本题综合考查了直线与圆,圆与圆的位置关系,切线的性质,直角三角形,相似三角形的判定等多个知识点.
(2)根据切线的性质容易知道O1D⊥PD,O2E⊥PE.由O1D∥O2E知:△PO1D∽△PO2E.
解答:
 解:(1)过点A作两圆的内公切线,交BC于点Q,
解:(1)过点A作两圆的内公切线,交BC于点Q,∵⊙O1与⊙O2外切于点A,直线l与⊙O1、⊙O2相切于B、C两点,
∴QB=QA=QC,
∴∠BAC=90°;
当l绕P点逆时针移动(过A点时除外),与⊙O1和⊙O2的交点从左到右依次为B、G、F、C时,∠BAC+∠GAF的度数能确定.过点A作两圆的内公切线,交BC于点Q;
∵⊙O1与⊙O2外切于点A,
∴∠GAQ=∠B,∠FAQ=∠P,
∴∠GAF=∠GAQ+∠FAQ=∠B+∠P;
∵∠BAC+∠B+∠P=180°
 ,
,∴∠BAC+∠GAF=180°;
(2)垂直线段:O1D⊥PD,O2E⊥PE
相似三角形:△PO1D∽△PO2E.
点评:本题综合考查了直线与圆,圆与圆的位置关系,切线的性质,直角三角形,相似三角形的判定等多个知识点.

练习册系列答案
相关题目
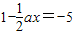 的解是偶数.
的解是偶数.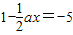 的解是偶数.
的解是偶数.

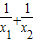 =( )
=( )